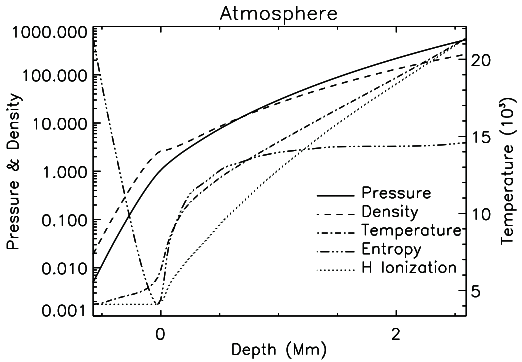
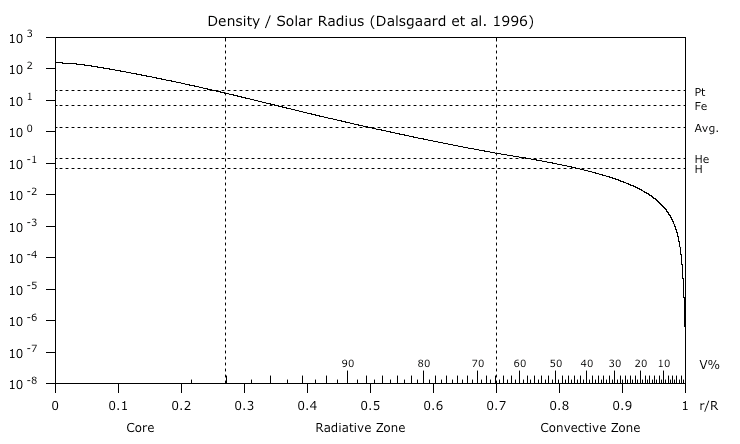
© Charles ChandlerSo now we turn our attention to the star about which we have the most information: our own Sun. The section on Tokamaks explained exotic stars as "natural tokamaks" (NTs). But while the Sun is of far more interest to us, it is not what astronomers would call exotic. And it's not a tokamak. The Sun's average magnetic field is about 1 Gauss, which is merely twice the strength of the Earth's magnetic field. For an object with 333,000 times more mass, proportionally speaking that's 1/166,500 the field. So the organizing principle is not magnetism, nor electrodynamics. But being less exotic doesn't make it any simpler. We have far more information about the Sun than we do for distant stars, and in the fine grain detail, there are many riddles.For example, Figure 1 shows the surface of the Sun "on the limb" (i.e., the horizon). Notice that the edge of the photosphere is very distinct, topped by the tenuous plasma in the chromosphere and transition region.1 At the surface, there is a marked change in the fluidity of the plasma, from the liquid-like surface, to the gas-like atmosphere.The liquid-like behavior of the surface becomes more obvious when we take a closer look. After the explosive release of energy in a solar flare, surface waves have been observed.2 This type of wave can only occur at the boundary between layers of dramatically different densities.3:73 (See Figure 2.)Figure 2. Waves propagating after a solar flare, 1996-07-09. The images show an area 200 Mm across.© 1998 SOHOYet in the standard model, a distinct surface just isn't possible. If the organizing principle is gravity, balanced only by hydrostatic pressure, the density gradient should be set deterministically by the ideal gas laws. (See Figure 3.)Figure 3. Density per solar radius in the Dalsgaard model, based on the ideal gas laws, with gravity pulling in, and with heat from nuclear fusion in the core generating the hydrostatic pressure that pushes back out. The X axis shows the decimal of the solar radius starting from the center, and the percentage of the solar volume, starting from the surface. The Y axis shows g/cm3. The densities of liquid platinum, iron, helium, and hydrogen are shown for reference. The average density of the Sun is 100.15 = 1.408 g/cm3 = 1408 kg/m3.The model density at 1.0 R⊙ (i.e., at the surface) is 2.00 × 10−4 kg/m3 (i.e., a good laboratory vacuum), increasing steadily to the density of STP air at a depth of 13.22 Mm. In such a smooth gradient, there is no distinct surface. Analogously, the Earth's atmosphere traverses the same gradient from the top of the mesosphere (i.e., the dashed red line in Figure 4) down to sea level.4 In this traversal, there are changes in composition that can become visible under the right conditions.Figure 4. Earth's atmosphere back-lit at sunrise. The pale blue-green color is from water vapor in the troposphere. The dark blue is from nitrogen and oxygen in the stratosphere. The dashed red line shows the top of the transparent mesosphere, where the density is just 2.00 × 10−4 kg/m3.© 2009 NASAFigure 5. Gravity waves in the Earth's atmosphere off the coast of Australia, 2003-11-11.© 2003 NASABut these are not surface waves, because the atmosphere has no distinct surface. Rather, these are "gravity waves" that move very slowly (typically at something like 10 m/s).5 The solar surface waves begin at a supersonic speed, and then accelerate, which is characteristic of a fundamentally different type of wave.While surface waves are rare, another form of hydrodynamics at the solar surface occurs all of the time (except when disrupted by sunspots): solar granules. (See Figure 6.) These have the appearance of thermal bubbles erupting onto the surface, as if an internal heat source were causing the liquid to boil. While the granules are typically about 1 Mm across, the altitudes of the tops are very consistent, typically being within .1 Mm of each other. Such precision is not expected when a liquid boils in a smooth density gradient. We would rather expect the larger bubbles to achieve a height above the norm in direct proportion to their size. Only a sharp drop-off in density at a surface can produce large and small bubbles that terminate at precisely the same elevation.More telling is that the hydrodynamics in such granules have been simulated, but it took a steep drop-off in density to get the dynamics right.6 (See Figure 7.) Clearly there are forces at work other than just gravity and hydrostatic pressure, or the density and pressure gradients would be straight lines on a log scale. So what are those forces?Since the ideal gas laws leave no room for reinterpretation, the only possible conclusion is that non-Newtonian forces are responsible for the density drop-off going from the photosphere out into the chromosphere. At the macroscopic level, there are two candidates: the electric force, and the magnetic force.We can rule out the magnetic force by several lines of reasoning. First, the Sun's magnetic field averages 1 Gauss, which is merely twice the strength of the Earth's average field, and there is no distinct density drop-off in the Earth's atmosphere due to the magnetic force. Second, hydrogen plasma doesn't have much of a magnetic dipole, so it wouldn't respond much, even to a strong field. Third, if it did, the surface of the Sun would vary with the strength and polarity of the magnetic field, which it does not.That leaves only the electric force. Since it's the only candidate, its presence need not be proved any other way (though it can be confirmed in many ways). The next section will determine the configuration of the electric force responsible for such a distinct edge.
1. Robitaille, P. (2011): On the Presence of a Distinct Solar Surface: A Reply to Hervé Faye. Progress in Physics, 3: 75-78 ⇧
2. Kosovichev, A. G.; Zharkova, V. V. (1998): X-ray flare sparks quake inside Sun. Nature, 393: 317-318 ⇧
3. Robitaille, P. (2007): A High Temperature Liquid Plasma Model of the Sun. Progress in Physics, 1: 70-81 ⇧
4. Picone, J. M.; E. Hedin, A.; Drob, D. P.; Aikin, A. C. (2002): NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. Journal of Geophysical Research, 107 (A12): 1468 ⇧
5. Gossard, E.; Munk, W. (1954): On Gravity Waves in the Atmosphere. Journal of Meteorology, 11 (4): 259-269 ⇧
6. Stein, R. F.; Nordlund, A. (1998): Simulations of Solar Granulation. I. General Properties. The Astrophysical Journal, 499: 914-946 ⇧




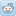





.jpg)