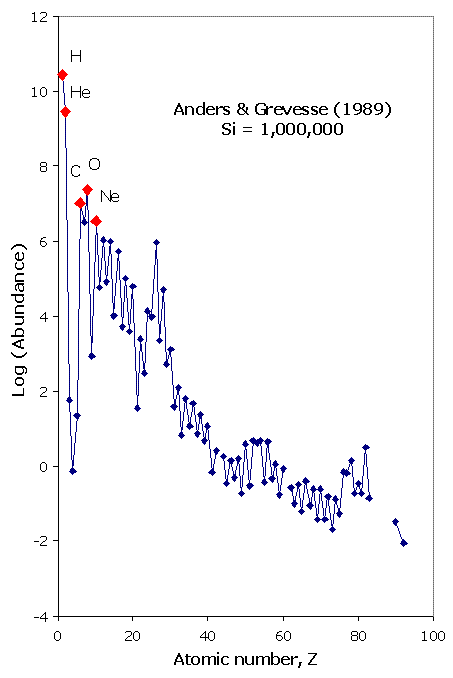
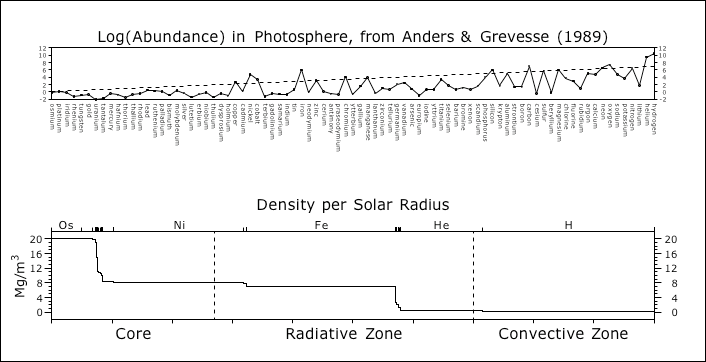
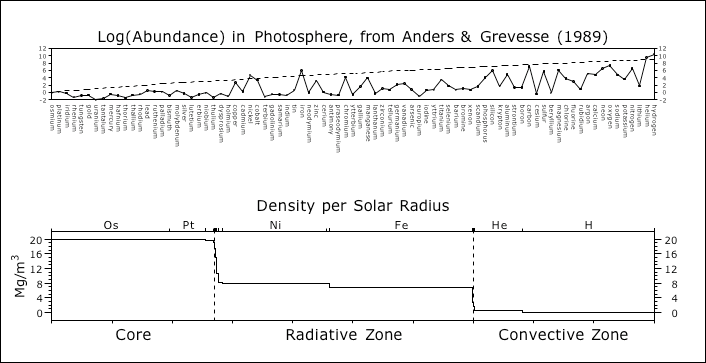
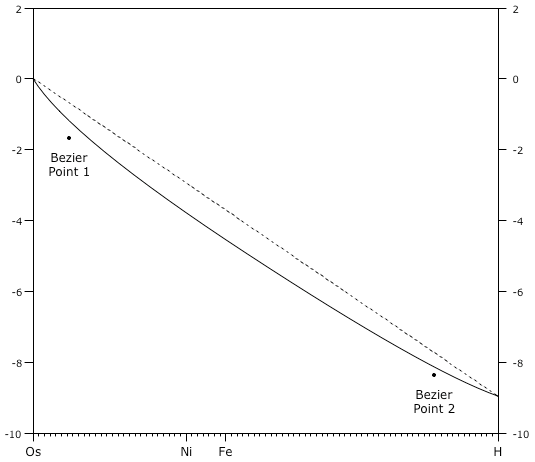
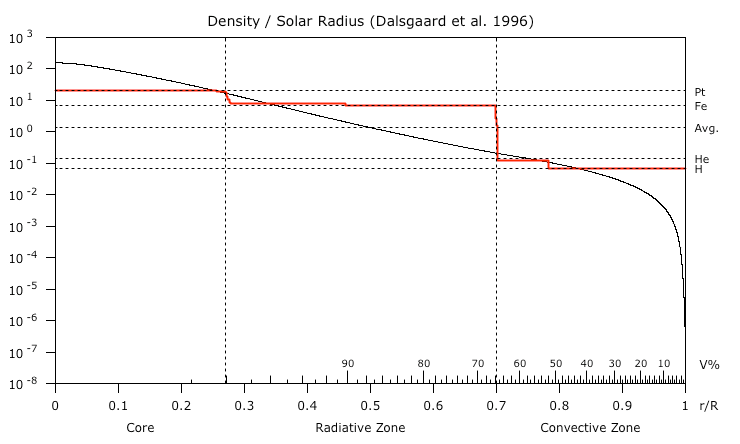
© Charles Chandler

 

The previous section established that electron degeneracy pressure (EDP) has to be taken into account if we are to understand the solar surface, since it is demonstrably charged, and the only way to sustain a net charge in the excellent conductivity of 6,000 K hydrogen, in the absence of a strong magnetic field, is with extreme gravitational loading. Under such pressure, electrons are squeezed out, leaving +ions behind. The electrons so expelled have nowhere to go but up, where the relaxed pressure affords sufficient space for them between the atomic nuclei. There will be a strong electric field between the +ions and the expelled electrons, but the charges won't recombine, because the gravitational loading won't let them. Thus current-free double-layers (CFDLs) have been instantiated. Above the negative layer, electric induction can organize yet another layer of opposite charge, which in this case is going to be positive, and which accounts for the positive charge at the surface. So the characteristics of the surface reveal the presence of at least two more layers of alternating charge beneath the surface.

 

Figure 1 shows that by the ideal gas laws, the pressure at a depth of 125 Mm is sufficient to compress hydrogen down to its liquid density. In the standard model, with hydrogen running all of the way to the core, the compression has to continue, eventually hitting 1538 kg/m³ at the solar center. But hydrogen at that density, just from gravitational loading, isn't physically possible. Compression beyond the liquid density expels electrons,¹ instantiating an electrostatic repulsion between the +ions. That repulsion is a strong deterrent to further compression. And while gravity is a respectable force inside the Sun, the electric force is 39 orders of magnitude stronger, meaning that the compression stops when the charge separation begins. Stuck at the liquid densities, the hydrogen should never get much above 76 kg/m³, which it achieves at a depth of only 125 Mm. Similarly, the helium achieves its liquid density of 145 kg/m³ at a depth of 176 Mm, and will forcefully resist further compression. The problem for the standard model is that there isn't any way of making up the average density of the Sun, which is 1408 kg/m³, if the helium never gets over 1/10 of that, and the hydrogen never gets over 1/20 of it.

 

There's really only one possibility here — to get more mass packed into a tighter space, without any additional force, we have to go with matter that has already been compacted beyond the Coulomb barrier and fused into heavier elements, which no longer need additional pressure to stay at that density.^2:76

 

How much heavier?

 

Simple calculations show that if the average density of the convective zone is that of liquid hydrogen, the average density of the core and radiative zone combined has to be 52 times greater.³ Iron's atomic mass is 55 times greater than hydrogen's, so at first blush, we might think that everything below the convective zone is just liquid iron. But there are two reasons for thinking that it isn't that simple.

 

Figure 2. Seismic shadows due to differences in density.

First, helioseismology reveals a distinct boundary at .27 R_⊙ that wouldn't be there if it was just one element below the convective zone. (See Figure 2.) So there must be an even heavier element in the core.

 

Second, we can see in Figure 1 that most of the radiative zone is above the density of liquid iron, which means that it's plasma, lighter than liquid. This makes sense if the temperature inside the Sun is at least 6000 K, because iron is only liquid below 4000 K at that pressure. And if most of the iron is plasma, lighter than liquid, something much heavier than iron has to be in the core to make up the total mass of the Sun.

 

So with hydrogen & helium in the convective zone, there are at least two other elements in the Sun (i.e., something heavier in the radiative zone, and something much heavier in the core).

 

Which elements?

 

We can guess at combinations of elements that might make up the mass of the Sun, but there is another type of data that can be taken into account that produces interesting results. In 1989, Anders & Grevesse did an excellent study of the spectrum of the Sun, detecting 92 elements.⁴ On the basis of the intensity of the spectral lines, they estimated the abundances of each element. (See Figure 3.)

 

 

Figure 3. Abundance of elements in the photosphere, dominated by hydrogen (10^10.45) and helium (10^9.46), based on the intensity of spectral lines.

 

 

This only tells us the abundances in the photosphere. But if there are traces of heavier elements in the photosphere, there are probably much larger quantities of those elements deeper in the Sun, assuming that most of the heavier atoms settled to the bottom.^5,6 So we can guess at the composition of the solar interior by assuming that it's made of the same stuff as the surface, just with higher proportions of heavy elements. In other words, if we were to estimate the composition of the Earth, and all we had was information about the troposphere, how would we go about it? The raw numbers tell us that the troposphere is 78% nitrogen, 21% oxygen, and 1% trace elements. But even if compressed by gravity into liquids, nitrogen and oxygen would still be too light to make up the total mass of the Earth. So there must be heavier elements in the Earth. Which elements? Having no other information, we can only look at the 1% trace elements, and assume that there are a lot more where those came from. Hence our best guess will be to re-scale the abundances, making up the missing mass by increasing the quantities of the heavier elements.

 

Figure 4 shows the Anders & Grevesse abundances, resorted by liquid density, and with the heaviest on the left. The dashes represent a new baseline for the abundances after they have been scaled. Hydrogen still dominates, but its abundance has been reduced by almost 10⁷. The abundances of all of the other elements have likewise been reduced, on a linear scale, proportional to their liquid densities. Reducing the lighter elements increases the heavier elements in the mix, achieving the target density of 1408 kg/m³. The lower panel then takes the new abundances, estimates the volume of each element given its liquid density, and then finds the radius of the Sun for each layer.

 

 

Figure 4. Abundances with linear correction for mass separation. (See the 11x17 PDF version.)

 

 

In the lower plot we can clearly see two large steps in density, from 1^st period elements (hydrogen & helium) at the top, to 4^th period elements (iron & nickel) in the middle, to 6^th period elements (platinum & osmium) at the bottom. This is interesting because helioseismology tells us that there are 3 distinct densities in the Sun: the convective zone, the radiative zone, and the core (as in Figure 2). But the steps in Figure 4 don't match up with the helioseismic boundaries. This suggests that we have the right idea, but we just need to fine-tune it a little bit. We have no reason to believe that the effects of mass separation have to be precisely linear. In order to know exactly how gravity stratifies elements in the Sun, we'd also have to know what is stirring up the mix, and this is information that we do not have. So it's possible that the scaling factor should be some sort of curve.

 

With heuristics it was determined that the simplest curve that gets the density steps to fall at the right places is a cubic Bezier with 2 control points. (See Figure 5.)

 

 

Figure 5. Abundances with bezier correction for mass separation. (See the 11x17 PDF version.)

 

 

The slight degree of curvature in the new baseline is barely visible in Figure 5, but can be more clearly seen in Figure 6. The tick marks on the X axis are for the same element list, sorted by liquid density, with the heaviest on the left. In this scheme, the abundance of hydrogen has been reduced by almost 10⁹, and all of the other elements have been scaled by the log factor given by the curve at each tick.

 

 

Figure 6. Bezier curve used to re-weight the Anders & Grevesse abundances, as shown in Figure 5.

 

 

Figure 7 shows these densities plotted on a log scale, compared to the Dalsgaard model densities.

 

 

Figure 7. Densities in the present model (thick colored line) compared to the Dalsgaard model (curve).

 

 

These calculations assume that all of the elements have been compressed into liquids. This actually produces too much mass. Yet only in the core, and in the bottom of the convective zone, is the pressure sufficient to liquify the elements there. So the flat-line densities of iron and hydrogen above their liquid lines in Figure 7 should actually have about a 2° slope, to get the target average density of 1408 kg/m³.

 

The net result is a fundamentally new conception of the solar constitution. It has the correct overall density, but it doesn't require elements to be compressed much beyond their liquid densities, which doesn't seem possible. With hydrogen being only 76 kg/m³, and helium being only 145 kg/m³, the only way to achieve the average solar density of 1408 kg/m³ is with greater quantities of heavier elements in the mix. Hydrogen still dominates, at 52% of the solar volume. But then there are large quantities iron & nickel in the radiative zone, and the core is comprised of osmium & platinum. With 1^st period elements in the convective zone, 4^th period elements in the radiative zone, and 6^th period elements in the core, wave propagation within the Sun will be affected, producing helioseismic shadows as have been observed. The actual radii of the helioseismic boundaries were then used to fine-tune the estimates of the elemental abundances.

 

Thus the model appears to be physics-constrained, meaning that the next step is simply to continue reading in more data, to see if the expected properties of the model continue to match up with the observations.

 

Calculations