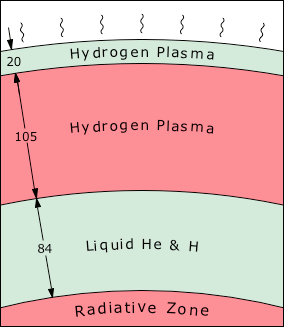
© Charles ChandlerWe know that for the electric force to have the influence described in the previous section, the top layer has to be charged.We can also deduce with confidence that there has to be a strong field between it and an underlying layer. If the Sun only had one charge (positive or negative), the Coulomb force would simply add to the hydrostatic pressure, somewhat more vigorously, and the density would thin out over a much greater distance. The only way to get densely packed plasma that suddenly stops at its outer extent is with an opposite charge below that is pulling it down forcefully. Hence there have to be "current-free double-layers" (CFDLs), where opposite charges cling to each other, but something is preventing recombination.CFDLs wouldn't seem possible in 6,000 K hydrogen, due to its excellent conductivity. But there are two known forces that can keep electric charges separate in the absence of electrical resistance. They are (obviously) the two other forces present at the macroscopic level: the magnetic force, and gravity. We already ruled out magnetism, so we'll investigate the effects of gravity.
Figure 1. Charge Separation Under Pressure
At left is an abstract representation of a normal crystal lattice, using the familiar icon for an atom, and showing connections of electron shells. At right, extreme pressure has forced the expulsion of one of the electrons from the atom in the center. The expelled electron is to be found just outside, wherever there is room for it, while attracted to the positive ion by the electric force.
Electron Degeneracy Pressure
$$P=\frac{h^2}{20m_em_p^{5/3}}\left(\frac{3}{\pi}\right)^{2/3}\left(\frac{\rho}{\mu_e}\right)^{5/3}$$ where: P = pressure h = Planck's constant me = mp = ρ = density μe = electron/proton ratio Thus the Pauli Exclusion Principle holds even for supercritical fluids. Monoatomic matter above the critical point isn't constrained by covalent bonds. But when two atoms are forcibly pushed together, the first conflict will be between the outer electrons. If the pressure is greater than the ionization potential of the atoms, the conflict results in the expulsion of electrons, leaving a strong electrostatic repulsion between the positively charged atomic nuclei, and further compression has to fight the Coulomb force. This marks the transition from compressibility to elasticity, which is very different. The Quantum Mechanics term for this effect is electron degeneracy pressure (EDP), though the Pauli Exclusion Principle predated QM, and is not reliant on it.If the pressure is coming from gravitational loading, it increases with depth, meaning greater compression, and atoms packed closer together. At the threshold for EDP, electrons are expelled, and they have nowhere to go but up, where they will find room between atoms that aren't as tightly packed. Thus the expelled electrons are forced to a higher altitude, leaving positive ions below.The implication not typically considered is that a charge separation has occurred, creating current-free double-layers (CFDLs) — they are layers of opposite charges, with a powerful electric field between them, but there is no current responding to the field, because something prevents it. Usually a sustained charge separation requires an insulator, but in this case, EDP separates the charges and keeps them separate. And gravity is forcing the EDP. So as long as those forces are present, there will be a charge separation, and an electric field.So we need to work out the implications of CFDLs inside the Sun.The inner layer is positive, due to the expulsion of electrons under extreme pressure. The liberated electrons congregate at a higher altitude. But that isn't the end of it. The negative layer so produced might go on to induce a positive charge in the layer above it, which will likewise be a CFDL, still in the presence of excellent conductivity. The positive double-layer will be attracted to the negative layer, but repelled by the positive layer below that (i.e., the one created by EDP), and all three will be stable in a positive-negative-positive (PNP) configuration. Such layers created simply by induction can continue ad infinitum, though in spherical layers, the charge density relaxes with each inversion. At some point away from the primary charge separation, the next induced double-layer will not be bound firmly enough to stay organized.So we have deduced with confidence the following facts.
- The electric force is responsible for the extreme density of the photosphere compared to the chromosphere.
- The photosphere is electrically charged.
- There is at least one other layer below it, with the opposite charge, supplying the force necessary to compress the photosphere far beyond the expectations of the ideal gas laws.
- The primary charge separation mechanism is electron degeneracy pressure (EDP), setting up the first two current-free double-layers (CFDLs). Additional layers might also be caused by induction.
We can also deduce the sign of the photosphere's charge, and the relative strength of its charge compared to the underlying layer. There are six possible configurations. There are two possible stacking orders (positive over negative, or negative over positive). Then there are three variations for the relative strengths of the charges (top layer is stronger, underlying layer is stronger, or the charges are perfectly matched).We can dismiss the possibility that the top layer has more charge, since the excess charge would simply drift away.We can also dismiss the possibility that the charges are evenly matched. In CFDLs, the electric field between the layers is greatest at the boundary between them. Moving away from the boundary, the field density diminishes, because of the increased distance from the opposite charge, and because of repulsion from like charges in the same layer. (See Figure 4.) Analogously, in a heavy element, the outer electrons are loosely bound, because of distance from the nucleus, and because of repulsion from electrons in inner shells. The same is true of plasma double-layers. The significance is that with equally matched charges in the solar double-layers, the density of the top layer would still relax gradually to nothing at some distance away. So the distinct limb proves that the underlying charge has to be more powerful, and the top layer has only its densest component. (See Figure 5.)
1. Saumon, D.; Chabrier, G. (1992): Fluid hydrogen at high density: Pressure ionization. Physical Review A, 46 (4): 2084-2100 ⇧
2. Dyson, F. J.; Lenard, A. (1967): Stability of Matter. I. Journal of Mathematical Physics, 8 (3): 423-434 ⇧
3. Lenard, A.; Dyson, F. J. (1968): Stability of Matter. II. Journal of Mathematical Physics, 9 (5): 698-711 ⇧
4. Dyson, F. J. (1967): Ground‐State Energy of a Finite System of Charged Particles. Journal of Mathematical Physics, 8 (8): 1538-1545 ⇧
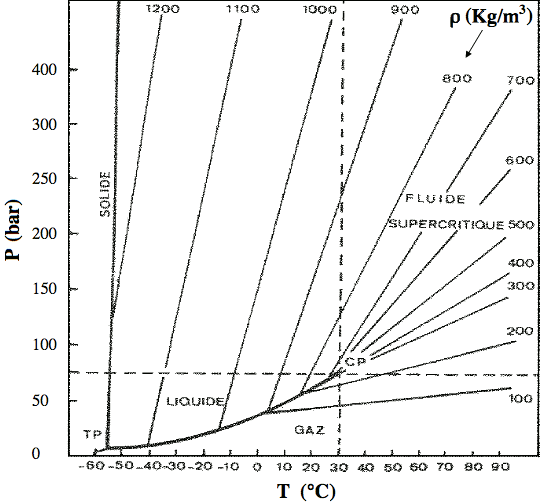
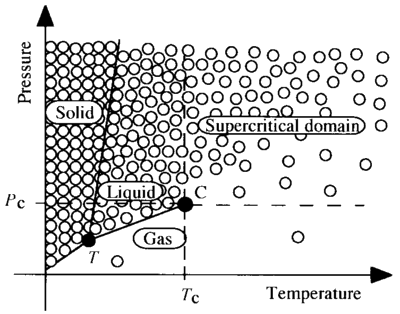
5. Otles, S. (2016): Supercritical Fluids — Density Considerations. ⇧
6. Tosatti, E. et al. (2009): High-pressure polymeric phases of carbon dioxide. Proceedings of the National Academy of Sciences, 106 (15): 6077-6081 ⇧
7. Weill, F. et al. (1999): Supercritical fluid processing: a new route for materials synthesis. Journal of Materials Chemistry, 9 (1): 67-75 ⇧
8. Kuhn, J. R.; Bush, R.; Emilio, M.; Scholl, I. F. (2012): The Precise Solar Shape and Its Variability. Science, 337 (6102): 1638-1640 ⇧