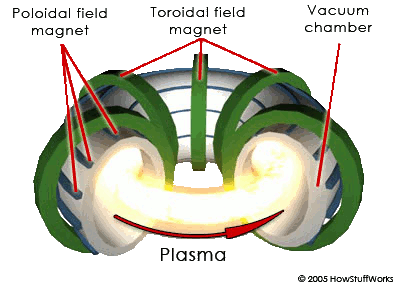
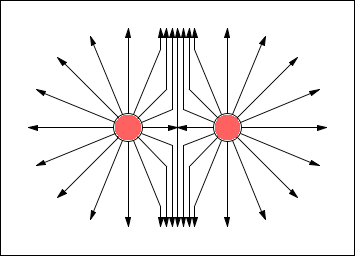
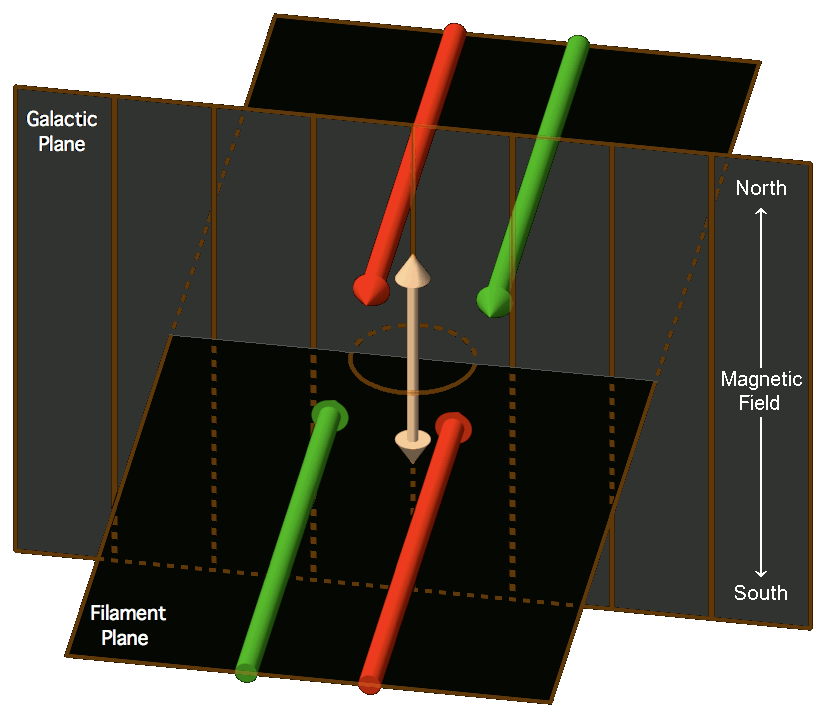
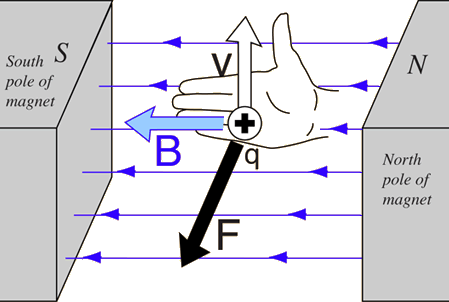
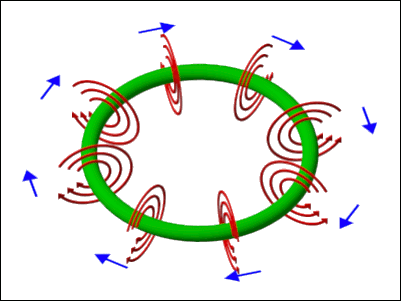
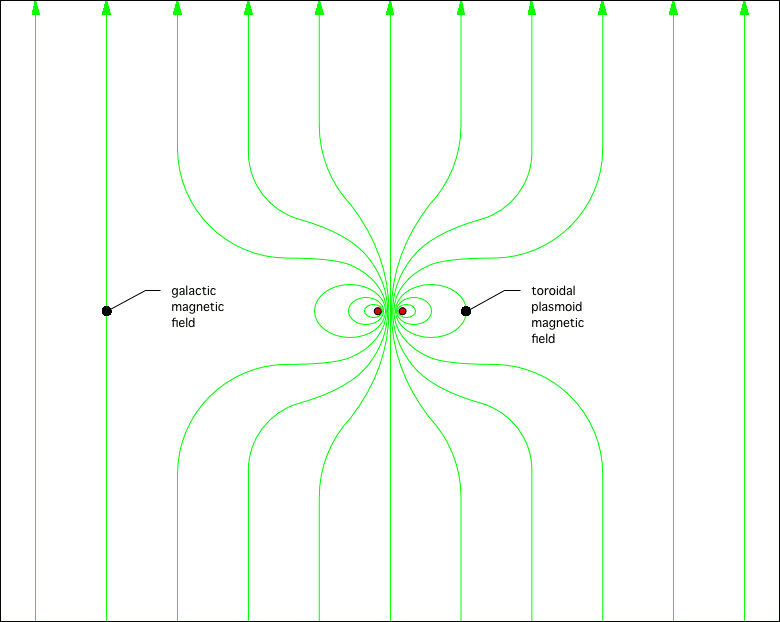
© Charles Chandler

 

The Filaments section established that imploding filaments of a dusty plasma can resolve into toroidal plasmoids. This section elaborates on the behaviors of such stars.

 

It was mentioned that the speed of the imploding plasma could be as high as 0.86 c (with the supporting calculations in the section on the Sun's Energy Budget). But note that this is just the speed of one half of the implosion (i.e., the rate at which each end of the filament moves toward the center). This means that the combined speed between opposing charge streams in the toroidal plasmoid will be double that — 1.72 c! At that rate, the magnetic pinch will be extremely robust, and the ohmic heating will create extreme temperatures — easily the conditions necessary for nuclear fusion.

 

This is interesting because one of the telltale signs of nuclear fusion in the laboratory is the release of gamma rays, and we certainly observe such radiation during the formation of certain types of stars. But in the standard model, such observations shouldn't be possible in space. Gamma rays are absorbed by the thinnest of gas clouds. We didn't know that anything at all was capable of producing gamma rays in space until we launched a satellite to detect nuclear explosions on Earth (to enforce the ban on nuclear weapons testing),¹ and it started detecting gamma rays that were not terrestrial. After 10 years of research, the conclusion was that the sources could only be celestial.² We now know that there are plenty of gamma ray sources in space, but they're only detectable from space, since the Earth's atmosphere absorbs the radiation. The significance is that there isn't anything between the Earth and the gamma ray source that is as thick as the Earth's atmosphere, or the radiation would have already been absorbed. Now if we consider what types of conditions are required for fusion, a very serious theoretical problem comes into full view — fusion does not occur in gas clouds thinner than the Earth's atmosphere — it requires extreme pressures. In the standard model, such conditions are present only in the cores of large stars, but the overlying matter will always absorb all of the gamma rays. So how can sustained fusion occur in space, when in at least one direction (i.e., facing us), there isn't anything as thick as our atmosphere containing the pressure?

 

Figure 1. Tokamak.

© 2005 HowStuffWorks

The possibility not previously considered is that the matter is being compressed by the magnetic pinch effect. In other words, the toroidal plasmoid has graduated into a sort of natural tokamak (or more aptly, a stellarator).³ (See Figure 1.) Of course, in nature there won't be any poloidal magnetic fields accelerating the plasma — all of the acceleration will have already occurred during the implosion of the linear filament, and the natural tokamak (hereafter, NT) will have only the conservation of that original momentum. But the magnetic pinch will be functionally identical, and with the same results — matter will be compressed to densities necessary for fusion. And since the magnetic force is transparent, we'll see the gamma rays.

 

Is there any other evidence of fusion?

 

Indeed there is. The central stars in planetary nebulae are known to fuse heavy elements,^4:199~207 and then eject them in bipolar jets. In the standard model, fusion occurs in the cores of large stars, but then the heavy elements should stay in the core, where their weight will prevent them from bubbling up through lighter elements toward the surface. So there isn't a way for heavy elements to even get to the surface, much less get there and then get accelerated above the gravitational escape velocity, never mind speeds that can exceed 100 km/s. Only an explosion of some sort could accomplish such acceleration. And yet what we see in planetary nebulae is a steady stream of particles. So it isn't one big explosion — it's an ongoing process, just with explosive power. For example, the lobes in Figure 2 took 1200 years achieve this size,^5,6 and some nebulae take as long as 20,000 years to form.⁷ This sounds a lot like sustained nuclear fusion. The standard model doesn't have such a near-surface energy source, but this isn't a problem for the NT model. If nuclear fusion is occurring, and since this tokamak doesn't have any walls, ejecta will escape the system. In other words, just as there isn't any overlying matter to block gamma rays, there isn't anything to block fusion by-products, such as energetic heavy elements.

 

 

Figure 2. Butterfly Wings Nebula (M2-9).

© 1997 NASA/ESA

 

 

More interesting still is the fact that the ejecta are collimated into bipolar outflows. This is extremely difficult to explain in the standard model. It is well known that the bipolar outflows follow magnetic field lines.^4:199~207,8 But the standard model can't explain what could create magnetic fields in this configuration, nor why the bulk of the matter would emerge from just two points on the star, instead of from all points equally, or from random points in turn.

 

Figure 3. Section of a toroidal explosion, looking along the plane of rotation, showing that 50% of the ejecta merge into "axial" jets (25% each way).

To begin to understand this, we can look at the geometry of a toroidal reactor that doesn't have any walls. (See Figure 3.) Nuclear reactions inside the torus will accelerate particles in all directions away from the annulus, but note that any particles ejected toward the center will collide with each other, and resolve into a collimated stream. The axial jets of a wide variety of star types then become explicable, including CSPNe, black holes, neutron stars, pulsars, magnetars, quasars, blazars, and white dwarfs, if they are all NTs.

 

In planetary nebulae, we have many more data from these near neighbors, and we can bring the picture into much clearer focus. In a recent study of the radio emissions from supernova remnants, it was found that almost all of the bipolar jets were aligned with their respective galactic planes, while the probability of this distribution occurring by chance is only 0.0007.^9,10,11,12 This is clear evidence of a force. Gravity isn't it, so it has to be electromagnetism. In spiral galaxies, the magnetic field is parallel to the plane of rotation. So the axial jets are parallel to the galactic magnetic field. The prevailing opinion is that this field is not strong enough to have dynamical effects on the central star, so the field steers the polar jets into alignment after ejection from the star. Yet in none of the cases is there any evidence of redirection moving away from the star, meaning that all of the "steering" would have to occur very near the star, when the ejecta are at their peak speeds. This is highly unlikely.

 

The NT model offers a more realistic possibility — the steering isn't getting applied to the ejecta (because the ejecta don't turn as they stream outward), and the steering isn't acting on the central star (because there is nowhere near enough force) — rather, the steering occurred earlier, acting on the filaments that collapsed into the central star, which just happened to set up an axis of rotation that was parallel with the galactic field.¹³ One estimate for the time that it takes for a dusty plasma to implode is 1.59 × 10⁸ years.¹⁴ That's long enough for electric fields measured in micro-volts per meter, and magnetic fields measured in nano-teslas, to influence the outcomes. If the external magnetic field can set the plane of rotation for the NT that will form, the jets will get a specific orientation relative to that field without any additional force.

 

So let's work backwards, from the outcome to the pre-conditions. (See Figure 4.) If the axial jets (shown in yellow) are to be parallel to the galactic magnetic field, the axis of rotation of the central star has to be parallel, meaning that the plane of rotation has to be perpendicular (shown as the circle in the middle of the image). And the imploding filaments have to be on the plane of rotation.

 

 

Figure 4. Filaments imploding on a plane that is perpendicular to the lines of force in the galactic magnetic field.

 

 

There is also a twist that needs to be set, such that the positive and negative strands of each half get separated on that same perpendicular plane. So Figure 4 shows the strands side-by-side, but if they were stacked one on top of the other, the plane of rotation would be vertical, and thus the axial jets would shoot out horizontally, not in line with the galactic field. So for this to work, the strands have to get separated left-to-right in this image.

 

Figure 5. The right-hand rule for the Lorentz force. With the thumb pointing in the direction of the moving positive charge, and with the other four fingers facing south in the external magnetic field, the Lorentz force is outward from the palm.

© 1998 GSU

Since the filament isn't going to split into positive and negative strands (due to magnetic pressure between the opposite charges) until the implosion has already begun and has developed a lot of speed, the direction of the split is determined by the external magnetic field. So we're looking for an effect coming from charged particles moving perpendicular to a magnetic field, that will get the positive charges to go one way, and the negative charges the other, on a plane that is perpendicular both to the field lines and to the particle motion. This is known as the Lorentz force. (See Figure 5.)

 

So if we are standing on the filament plane, with our feet pointing south in the galactic magnetic field, and facing in the direction of one of the imploding filaments, the positive component will get deflected to our left, while the negative component will go to our right. Coming in from the opposite direction, it's the same thing, except that the directions are reversed. Thus the positive stream coming from one direction always collides with the negative stream coming from the other direction. The Filaments section established that nearing the collision, there are both electric and magnetic reasons for the charge streams to prefer collisions with their opposites, but the present point is that this has already been determined, and the orientation has been set. If an NT forms, its axis of rotation will be parallel to the external magnetic field, and thus the axial jets will be generated parallel to that field.

 

To complete the concept, we can wonder what put the start points of the filaments on a plane perpendicular to the galactic field in the first place, because if that isn't set properly, there will be no way to get the axial jets parallel to the galactic field. But that might be the wrong question — it might just be that any filament that implodes on a plane that isn't perpendicular to the galactic field won't get separated into strands by the Lorentz force. If the filament implodes on a plane that is parallel to the galactic field, the Lorentz force will simply set positive and negative charges into helical paths. As such, the strands won't get separated side-to-side, and then the pre-conditions for a toroidal plasmoid will not be present. So filaments imploding perpendicular to a strong galactic field will get that side-to-side strand separation that makes them candidates for resolving into NTs, while any other orientation will result in the formation of a main sequence star.

 

Figure 6. Solenoidal magnetic field formed by rotating current.

Now we can see what coerces the galactic magnetic field lines into the classic hourglass shape, which defines the form of the bipolar jets.

 

Once the NT gets established, with relativistic angular velocities, it will generate its own magnetic field. For a ring current, the B-field is in solenoidal form. (See Figure 6.) If we grab the near side of the ring with a right hand, the thumb will point in the direction of the positive current, and the 4 fingers will point south in the toroidal B-field. So south is down in the center, and up around the outsides. If we return to Figure 4, we had a galactic magnetic field with south facing down, which deflected positive charges to their left, setting up the rotation, with positive charges going clockwise, as they are in Figure 6. Thus the interior solenoidal field of the NT is compatible with the galactic field, while the exterior is contrary.

 

The NT field will then perturb the galactic field, as depicted in the following images. Figure 7 shows the straight lines of the galactic field. Figure 8 shows the lines of force around the outside of the toroid, which are similar to those of a bar magnet. Figure 9 shows that field superposed on the galactic field, producing the hourglass form. (All three figures were generated using one of Paul Falstad's EM applets.)

 

 

Figure 7. Lines of force in the galactic magnetic field.

Figure 8. Lines of force around the outside of a solenoid.

Figure 9. Solenoid superposed on the galactic field.

 

 

Figure 10 shows the same thing as Figure 9, but in schematic form (i.e., not computed). The shortest, densest lines of the toroidal field close locally, while the longer lines are more susceptible to interception by the external field.

 

 

Figure 10. Section through a ring current (in red) generating a magnetic field (in green) that perturbs the straight lines of an external field.

 

 

Figure 11 shows a blow-up of Figure 10, along with the initial trajectories of the particles ejected from the NT (as in Figure 3). The ejecta will be +ions, and as such, they will tend to follow magnetic lines of force (i.e., as Birkeland currents).¹⁵ These "currents" are responsible for the radio emissions from planetary nebulae, since the helical motion of charged particles in a field-aligned current generate cyclotron radiation. The text following the image describes the expected behaviors of the ejecta traveling in each direction.

 

 

Figure 11. Particles ejected from a "natural tokamak" (NT), and the magnetic field lines that they will tend to follow.

 

 

Figure 12. The "shuttle ball" game, where the contestants pull the strands apart to accelerate the shuttle away from them.

© 2021 BOHS

First, what becomes of the collimated axial jets? If it were not for the galactic field, we'd expect the jets to stay organized — indefinitely if they don't collide with anything else — bound together by their collective magnetic fields (i.e., the magnetic pinch effect). But if there is an external field, the splaying lines of force do not lose their strength, and we have to consider the effects of that splaying. Charged particles spiraling around magnetic field lines behave as bar magnets, which are accelerated in the direction of converging field lines, and thus are decelerated in diverging lines. One way to think of this is to imagine a ring with strings passing through it — if the strings are diverging, the ring won't want to go in that direction — the force of divergence will rather send the ring sliding down the strings in the direction of convergence. (See Figure 12.) So if the axial jets are encountering the deceleration of Birkeland currents in a diverging magnetic field, the highly collimated, fast moving jets will break down into high pressure bubbles that will propagate slowly away from the center thereafter. This explains the bipolar internal bubbles in Figure 2, as well as in the Ant Nebula, and the Eskimo Nebula (in which we are looking along the axis of rotation, down the middle of the cylinder).

 

Second, we should consider what happens to particles that are ejected straight out, along the plane of rotation. These will encounter magnetic braking, as they attempt to move perpendicular to the magnetic field lines. Thus we would expect an accumulation of matter on the plane of rotation. And indeed, this is sometimes observed.¹⁶ But note that the present model doesn't have such matter as part of an "accretion" disc — rather, it's an excretion disc. The matter that formed the star was in a filament that resolved into an NT. The accumulation of matter on the plane of rotation didn't begin until after the NT got lit and started ejecting heavy elements. And that matter isn't flowing in, fueling the star — it's flowing out, as fusion by-products. (Iron is a poor choice of fuels for a tokamak.) And it makes sense that the mass of the "excretion disc" is just a few percent of the mass of the bipolar lobes¹⁷ — only the matter ejected on the plane of rotation is going to accumulate — everything else escapes the star's gravity, and proceeds outward.

 

Lastly, we see that between the polar and equatorial directions, particles are moving diagonally to the lines of force. These particles will be deflected in the direction of those lines, and go on to form the cylinder of the nebula. And while these particles initially experience deceleration due to the splaying magnetic field, once they get to the shoulder of the cylinder, the lines of force then converge. Thus there will be an acceleration into the main body of the cylinder, which shows up as a violet ring in Figure 2. And this explains why the cylinder projects further from the source than the remnants of the axial jets — the particles flowing into the cylinder got accelerated, while the axial jets experienced only deceleration.

 

Bipolar Planetary Nebulae Gallery

Hello — tokamaks don't work!