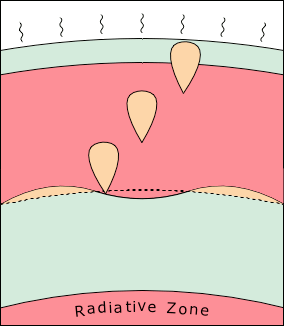
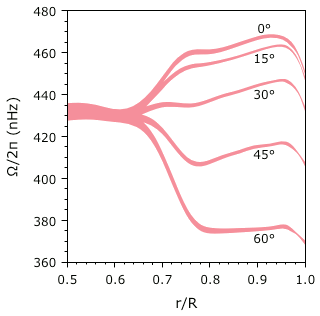
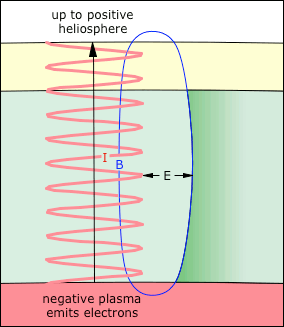
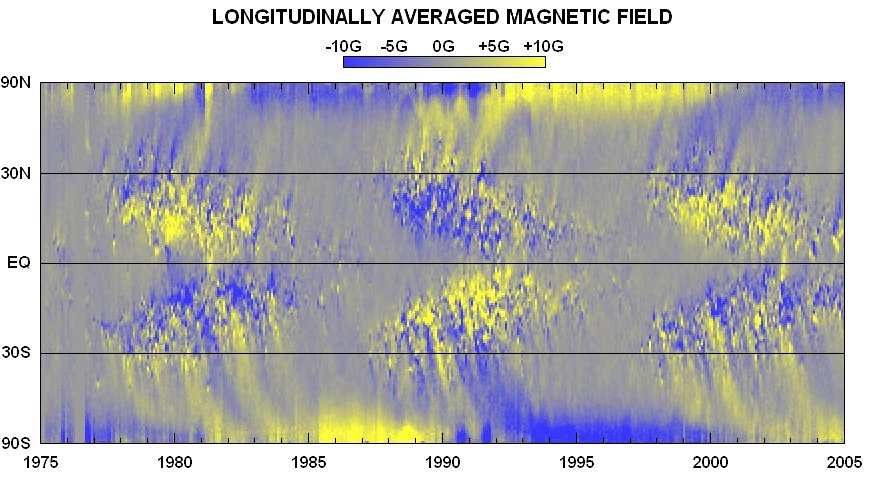
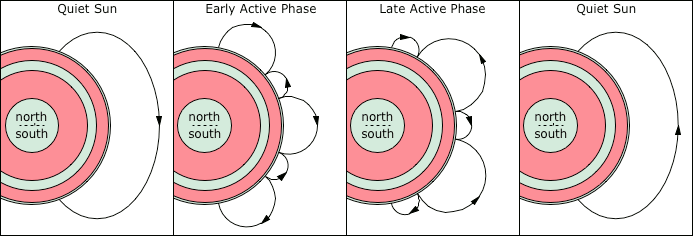
© Charles ChandlerLastly we will challenge the present model to explain the solar cycle. There are a lot of data, because the cycle is complex, but there really isn't a standard explanation for all of it to give us some competition. So the challenge is simply to see if the present model can identify mechanisms that would produce the broad range of observations, without violating any fundamental principles of physics.The first fact is that the total solar power output varies approximately 0.1%, on an 11.2 year cycle.1 The true significance of those numbers is easy to miss in the solar literature, but the reality is that it's a very slight difference, over a long period of time. Hence we shouldn't be looking for powerful mechanisms that throw the Sun into wild fluctuations. Rather, we should be curious about what keeps the power output so consistent. In that context, the study of the solar cycle is a search for near-perfect power regulator(s) whose nature(s) can be clarified by understanding the minimum and maximum output modes.The most obvious aspect of the cycle is the number of sunspots. The Sunspots section explained these as electric currents similar to the current flowing through the granules, but with a greater current density, such that electrodynamic effects emerge, including self-stabilizing solenoidal magnetic fields. So why is there a cyclic increase in current density?First we should consider where sunspots occur. The convective zone has an equatorial band, spanning 30° N to 30° S, that rotates faster than the polar caps. Sunspots occur in the boundary between these masses. (See Figure 1.) As the sunspot maximum proceeds, the width of this band shrinks, eventually spanning only 5° N to 5° S, bringing the sunspots nearer the equator. So something about differential rotation is definitely conducive to sunspots, and the increased current density then produces 0.1% more power.Some have suggested that boundary vortexes resulting from differential rotation encourage sunspots.2 But sunspots rotate extremely slowly, if at all, questioning the significance of vorticity. So we need to make a more detailed analysis, starting with what creates differential rotation in the first place.The core and the radiative zone rotate as solid bodies. In the absence of convection (because of a lack of a heat source), all relative motion has ceased. But in the convective zone, relative motion does exist, and we wouldn't expect solid body rotation. Yet what happens doesn't match the initial expectations.Given the conservation of angular momentum in an updraft, it should rotate slower than the plasma into which it rises, producing an apparent retrograde deflection. Figure 2 depicts an equatorial section looking down from the north pole, where the frame rotates counterclockwise with the Sun over a 3.62 day period. The s-wave at the bottom left generates a supergranule that should appear to move diagonally to the right as it rises. Similarly, downdrafts should rotate faster than the plasma into which they descend. So the upper convective zone should rotate slower than the solid body rate.The deceleration of updrafts and the acceleration of downdrafts certainly happen in the topmost 25 Mm.3,4,5 (See Figure 3.) This suggests that there are robust convective currents in the topmost positive layer, driven by ohmic heating from the solar~heliospheric current.Below 25 Mm, simple expectations are not met. In the lower latitudes, we actually see an acceleration, above the solid body rotation. And then in higher latitudes, where there is less angular momentum to conserve, there is an even more dramatic deceleration.
1. Willson, R. C.; Hudson, H. S. (1991): The Sun's luminosity over a complete solar cycle. Nature, 351 (6321): 42-44 ⇧
2. Zhao, J.; Kosovichev, A. G. (2004): Torsional Oscillation, Meridional Flows, and Vorticity Inferred in the Upper Convection Zone of the Sun by Time-Distance Helioseismology. The Astrophysical Journal, 603: 776 ⇧
3. Vorontsov, S. V. et al. (2002): Helioseismic Measurement of Solar Torsional Oscillations. Science, 296 (5565): 101-103 ⇧
4. Korzennik, S.; Thompson, M. J.; Toomre, J. (1997): Internal rotation and dynamics of the Sun from GONG data. Proceedings of the 181<sup>st</sup> Symposium of the International Astronomical Union ⇧
5. Basu, S.; Antia, H. M. (2003): Changes in Solar Dynamics from 1995 to 2002. The Astrophysical Journal, 585: 553-565 ⇧
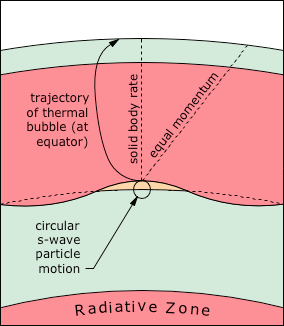
6. Miesch, M. S. (2005): Large-Scale Dynamics of the Convection Zone and Tachocline. Living Reviews in Solar Physics ⇧
7. Charbonneau, P. et al. (1999): Helioseismic Constraints on the Structure of the Solar Tachocline. The Astrophysical Journal, 527: 445-460 ⇧
8. Lanza, A. F. (2007): Angular momentum conservation and torsional oscillations in the Sun and solar-like stars. Astronomy & Astrophysics, 471 (3): 1011-1022 ⇧