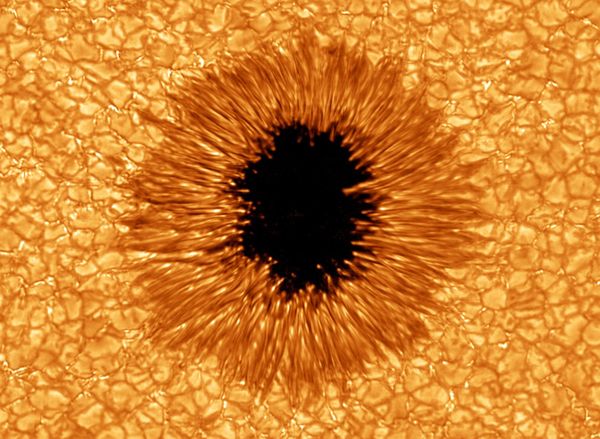
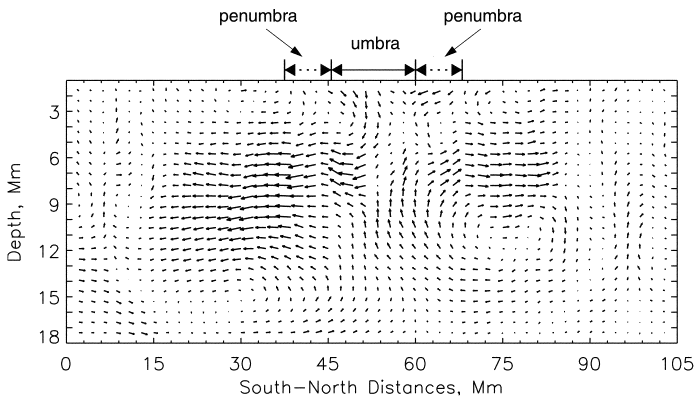
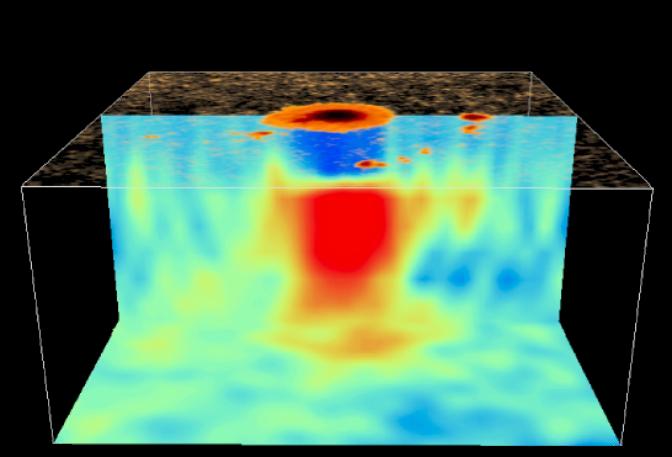
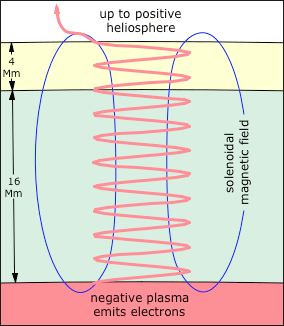
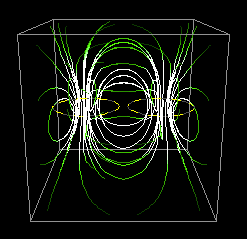
© Charles Chandler

 

Aside from granules, the other distinctive pattern in the solar surface is sunspots. In classic form, these have a roughly circular interior, called the umbra, surrounded by filaments that arc up, out, and then back down into the granular layer. The filaments are known collectively as the penumbra. (See Figure 1.)

 

 

Figure 1. Sunspot, courtesy New Jersey Institute of Technology's New Solar Telescope.

 

 

Figure 2. In a solenoid, a rotating electric current generates axial lines of magnetic force.

The key to understanding sunspots is their magnetic fields.¹ The lines of force rise up through the center of the sunspot, and then splay outward above the surface. So what is the magnetomotive force?

 

As the convective zone is comprised of 75% hydrogen and 25% helium (neither of which have strong magnetic dipoles, especially in the plasma state), the particles in question are not magnetized, and the field cannot be coming from frozen-in dipoles.

 

The only other way to generate a powerful magnetic field is with an electric current. When we see the greatest field density along the axis of a roughly circular form, we know that it's a solenoid generated by a rotating current. (See Figure 2.) Since there is no evidence of the plasma itself rotating fast enough to generate the field densities in question, the solenoid can only be evidence of a flow of electrons through the excellent conductivity of the plasma, where the positive ions remain relatively stationary.

 

Indirect evidence of the rotating electric current includes the migration of granules away from sunspots (indicating a submerged heat source, such as ohmic heating under the penumbra, as in Figure 3), and the Wilson depression in the center of the umbra (where less ohmic heating leaves the plasma cooler, and thus heavier, so it settles).

 

 

Figure 3. Plasma flows under a sunspot, indicating a heat source from roughly 18 Mm to 4 Mm below the surface.

 

 

Note that the updrafts in Figure 3 level off at about 4 Mm from the top, and then splay outward. This is one of the lines of evidence that there is a layer of thick plasma below 4 Mm, topped by a very thin layer of granules — otherwise, the updrafts wouldn't mushroom at a depth of 4 Mm.² Some of the literature refers to this density ledge as the difference between the actual "surface" of the Sun, versus its "atmosphere." In the present model, there is definitely a distinct change at 4 Mm, from high-density plasma issuing blackbody radiation, to low-density granules that absorb specific frequencies in that radiation. The depth of the granular layer is estimated at 4 Mm by the typical dynamics of thermal bubbles (i.e., depth = width × 4), which the helioseismic data confirms. But the thick plasma below 4 Mm is still above its liquid density, so calling it a "surface" isn't substantially more accurate.

 

Measurements of the sub-surface speed of sound confirm that the cooler umbra is roughly 4 Mm deep, and that the sunspot shaft below that is hotter than the surrounding plasma.³

 

 

Figure 4. View of the 3-D structures below a sunspot, based on wave transmission speeds, courtesy Kosovichev et al.

 

 

Figure 5. Schematic diagram of a sunspot.

The other significance of these helioseismic data is that they set a depth of ~20 Mm for the sunspot shaft. So in the present model, that's where the electric current starts, defining the upper limits of the negative layer. (See Figure 5.)

 

What's the electromotive force?

 

In the Granules section, a steady flow of electrons was identified, from the negative layer in the convective zone, up through the 20 Mm positive double-layer on top of it. (See Figure 6.) It was noted that this current starts slowly, accelerating as it moves away from the current divider. Because of the slow speeds, we don't typically see electrodynamic effects. Due to electrostatic repulsion, the electrons are well distributed, and they just drift slowly toward the surface and then on out into space. But in sunspots, electrodynamics are present and distinctive. Hence the electric current in a sunspot is the same electron drift that emanates from all points on the Sun, but the current density is greater, and an organized form emerges.

 

The next question is, "What induces the rotation in the electrons as they rise up through the sunspot, resulting in a solenoidal field?" They certainly aren't following the wraps in a coil of wire.

 

The most plausible answer is that it's the Lorentz force. Where sunspots occur, the Sun's magnetic field is perpendicular to the surface. Electrons shooting straight up through a sunspot will generate magnetic fields in conflict with that pre-existing field. If the electrons spin as they go, the fields come into agreement. (In other words, it forms a Birkeland current.) Due to magnetic pressure within the spiral, the spin is flattened, resulting in more turns to achieve the same vertical motion. The result is a solenoidal field that is actually far stronger in its axis than the external field — up to 4000 times stronger!

 

Still, the general sense of the electric current is from the negative layer outward into space, and this explains a curious fact about the sunspot's magnetic field. The central lines of force are "open," meaning that instead of closing within the solenoid, they project out into space. (See Figure 7.) This shouldn't be possible, but if that's the overall direction of the current, solenoidal lines that should have closed locally can get distorted into axial fields in Birkeland currents, which never "close" in the same way.

 

 

Figure 7. Coronal loops and open flux tubes.

 

 

Figure 8. AR 9169, 2006-06-11, seen in 171 Å, courtesy TRACE.

 

 

Yet we also see electric currents that ignore the overall electric field, and prefer to flow through the penumbral filaments toward the surrounding granular layer (as in Figure 1). The evidence of these currents is that on one side of each filament, the solenoidal field is deflected downward, and on the other side it's upward. Hence there is a circular Ampèrian field generated by a current through the filament.⁴

 

These penumbral electric currents don't make sense until the entire context is considered. The dominant electric field is between the negative layer below and the positive heliosphere above. Not considering electrodynamics, the electron drift should be straight up. But once the solenoidal configuration is instantiated, electrons moving outward toward space have to cross their own magnetic field lines to get there. This introduces a new Lorentz force that deflects the electrons into spirals around the solenoidal lines. (See the deflected path at the top of Figure 5.)

 

Now if we look carefully at Figure 1, we see that the penumbral filaments have no footpoints at the outer ends. The granules outside of the sunspot seem relatively unaffected, even by filaments that arc across their tops. So where do the penumbral currents go? To answer this, we have to remember that the electric field is between the Sun and the heliosphere. With an added Lorentz force, the current can be deflected. But the solenoidal lines close within the Sun, and if the current kept following them, it would be taken back down, into the Sun. This would have the current flowing against the electric field. So once the current gets to the top of a filament, the electric field starts decelerating the current. With decreasing velocity, the current's Ampèrian field diminishes, leaving it less subject to the Lorentz force. Then the electrons are dispersed by their own Coulomb force, and are free to respond simply to the solar~heliospheric electric field. Hence the tapering filaments are evidence of their relaxing current density, and they do not discharge into the granules at all.

 

The deflection of the current also answers the obvious question of why we don't see evidence of an increased current density in the chromosphere above a sunspot. Once the current gets past the resistance inside the Sun, its velocity should increase dramatically, and the current should get pinched into a discrete discharge channel. In other words, there should be a spicule on top of every sunspot, but this is not what happens. Yet a decreasing current density, and an absence of spicules, is expected in the presence of a solenoidal field, whose lines splay outward. Currents following those lines will get less dense, not more.

 

Hidden in this is a more interesting question. If the magnetomotive force is a solar~heliospheric current, why do the lines of force close in such small loops? The axis of the solenoid should stay organized, and in fact, it should get stronger, as the current accelerates out into space. This shouldn't form a solenoid just within the Sun — the magnetic field should be as big as the current itself.

 

Yet the current has to pass through the granular layer, which is cooler. Electron uptake in this layer represents an increase in resistance to the current. So the electron drift velocity is reduced. Also, while the net field is between a negative layer inside the Sun and the positive heliosphere, there is a fluctuation in that field due to the topmost layer of positive charge — at the bottom of this layer, the positive charge adds to the overall field, while at the top, it detracts from it. So the electrons move quickly at first, until they get to the top of the positive layer, where they slow down a bit, still moving outward, but less vigorously than they started.

 

The result is that the magnetic field density relaxes. This allows the stronger field lines already generated to close locally. When they do, the current out of the top is further decelerated by the braking effect of the penumbral Lorentz forces, further reducing the magnetic field in and above the granular layer. So the whole thing resolves into a local solenoid, instead of an interplanetary one.

 

Figure 9. Closing field lines in reversed solenoids.

The next topic is sunspot pairs. The primary sunspot's field has the same polarity as that hemisphere's pole, but the secondary sunspot's polarity is always reversed. This is because the secondary sunspot forms in the presence of an overall field that is opposite. While the Sun's overall magnetic field, at 1 Gauss, sets up the Lorentz force that induces the rotation in the first sunspot, the rotating current generates a 4000 Gauss field. (See Figure 2.) Where its closing lines of force dive back into the Sun, the dominant magnetic field is opposite from the Sun's overall field in that hemisphere. If another sunspot forms in the presence of that polarity, its electrons will spiral in the opposite direction, to generate a magnetic field that agrees with those lines of force.

 

The two sunspots then make a pair that is much stronger, as neither has to fight back-pressure in the surrounding granular layer. (See Figure 9.) In both cases, the prime mover is the electric force that induces a flow of electrons upward, and the physical characteristics (i.e., width, Evershed flow, Wilson depression, etc.) are roughly the same for either polarity. The only difference is which way the electrons rotate as they climb up through the convective zone.

 

Figure 10. Taken by Hinode's Solar Optical Telescope on 2007-01-12, this image of the Sun reveals the filamentary nature of the plasma connecting regions of different magnetic polarity.

Between sunspots there can be filaments (also called "prominences" when viewed from the side). (See Figure 10.) These filaments definitely match up with the magnetic field lines that have been measured, so there is no doubt that the EM configuration is like that shown in Figure 9.

 

Typically the filaments are described as magnetized particles in "magnetic flux tubes," like beads sliding down a string, but this is not correct. With weak magnetic dipoles, hydrogen and helium plasma wouldn't be moved much anyway, even in extremely powerful magnetic fields. Furthermore, magnetic fields can only accelerate magnetized particles where the lines of force are converging, and the acceleration is only in the direction of the convergence. Hence there is no way to accelerate magnetized particles out of one pole and into the other, and the ferromagnetic analogy is truly no help here. In superheated hydrogen and helium plasma, all of the magnetic fields come from the flow of charged particles, by Ampère's law. When we see particles flowing along magnetic field lines, we know that it is a B-field-aligned current, wherein the particles spiral to get their magnetic fields lined up with the external field, which in this case is the double-solenoid field. The actual amount of current in these "flux tubes" is substantial compared to the total discharge at the top of the sunspots. (The average solar current density, as the total current divided by the surface area of the Sun, is 2.93 × 10¹⁵ A / 6.09 × 10¹⁸ m² = 5.40 × 10⁻⁴ A/m², while in the filaments, it's in the range of 1~3 A/m².^5:11) Sunspots are of opposite magnetic polarity, but of like electric polarity, so strong currents only flow along these filaments when the charge balance has been disrupted by a solar flare.

 

Another interesting aspect of sunspot pairs is that the "leading" sunspot always has the magnetic polarity of that hemisphere's pole, while the "trailing" sunspot's polarity is reversed. ("Leading" means ahead, in the direction of the Sun's rotation.) This implies that both sunspots sprang from a hotspot deeper in the convective zone, such as at the liquid hydrogen line. The first upwelling of hotter, more conductive plasma to reach the surface provides a conduit for electrons that rotate in a direction consistent with that hemisphere's overall magnetic field. The second upwelling, arriving later and therefore emerging "behind" the first due to the conservation of angular momentum in the updraft, does so within the closing magnetic lines of force of the first sunspot. Hence the electrons in the trailing sunspot rotate in the opposite direction.

 

One final detail is worth noting. The umbra of a sunspot is cooler than the surrounding granular layer, issuing blackbody radiation in the range of 3000~4500 K, compared to the typical 5525 K radiation from the rest of the Sun. (See Figure 1.)

 

When combined with the fact that the center of the umbra is typically 700 km below the tops of the granules (i.e., the Wilson depression), the standard model has it that the layer generating the 5525 K radiation is only 700 km thick, and the sunspot somehow parts this layer, revealing the cooler convective zone beneath. In other words, the belief is that the underlying temperature is 3000~4500 K, while in the topmost 700 km, the temperature jumps up to 5525 K. If a sunspot is there, we peer into what we can't see otherwise. This is an odd piece in the standard model, which has all of the energy propagating outward from the core. If we could peel back the outer layer, we should see higher temperatures, not lower.

 

Then, when combined with "limb darkening" (as presented in the Granules section), the standard model is stretched to the breaking point, because the temperature profile in the topmost 700 km would be 3000~6400~4600 K. It's hard to believe that such a stratification would be possible when also remembering that granules redistribute the heat in this layer every 20 minutes. So all of the energy would have to be converted within that 700 km layer. Yet the standard model has heat convecting to the surface. Furthermore, what kind of conversion could be occurring in hydrogen plasma, only when it gets to a density 4 orders of magnitude thinner than STP air?

 

It's far more reasonable to consider that the Sun is transparent to a far greater depth, and that the 4600~6400 K blackbody radiation is coming from a depth of 4+ Mm. As the granular layer is thinner, the temperature should be less, and cooling enables charge recombination. Once neutralized, the atoms become capable of photo-ionization, which explains the absorption lines in the solar spectrum. The net result is that we shouldn't expect a major temperature difference in the Wilson depression just on the basis of heat stratification.

 

The present construct offers another explanation. The Lorentz force induces a rotation that gets the electrons out of the umbra and into a spiral under the penumbra, meaning less ohmic heating in the umbra. 3000 K is then the temperature of the granular layer with an unusually weak electric current running through it.

 

Discussion