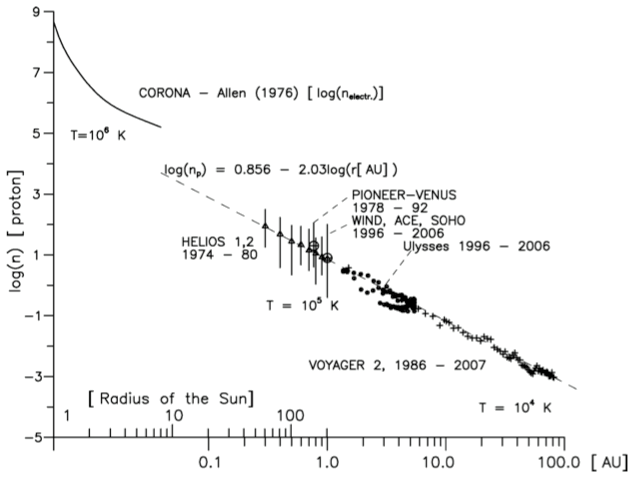
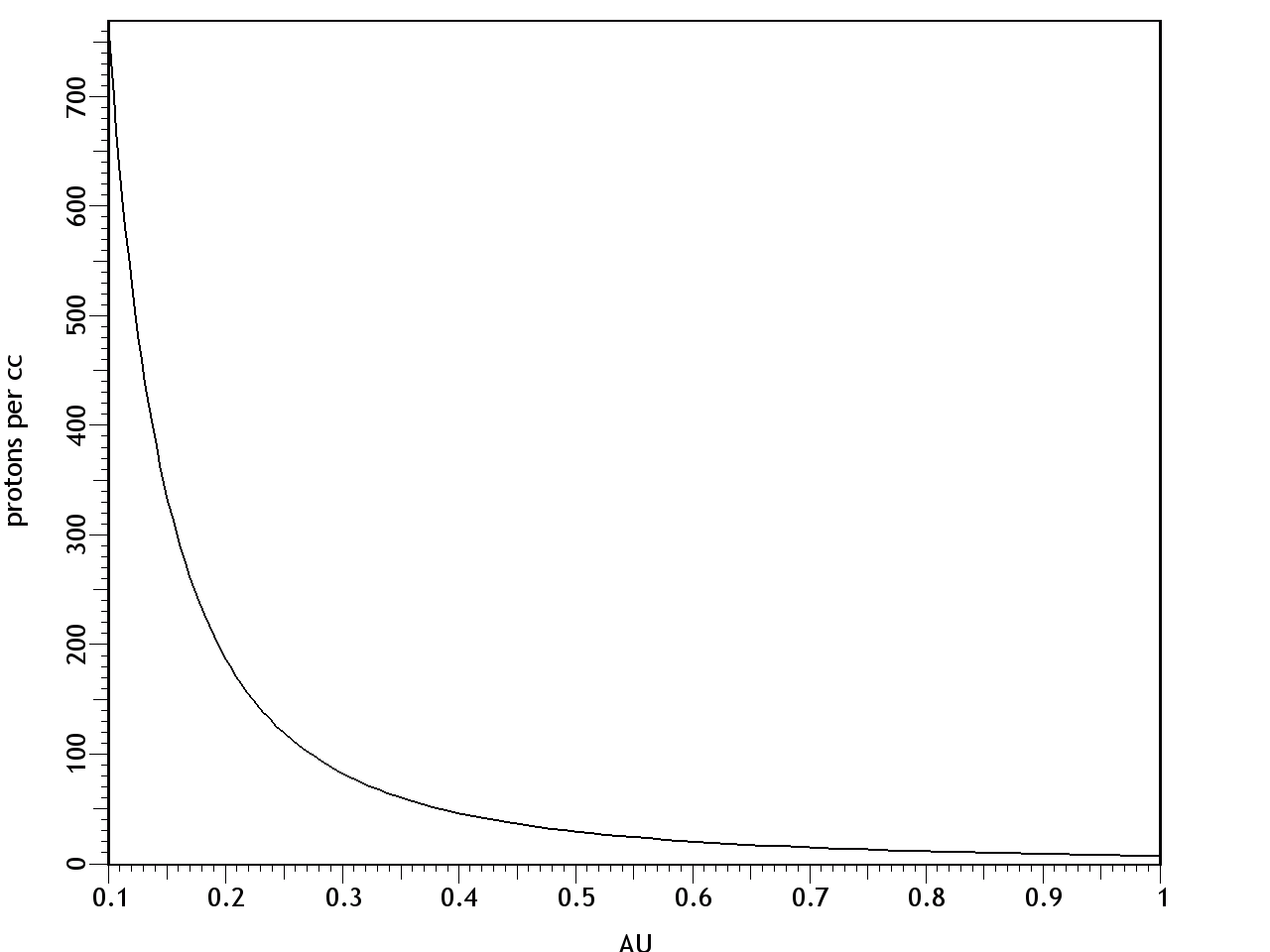
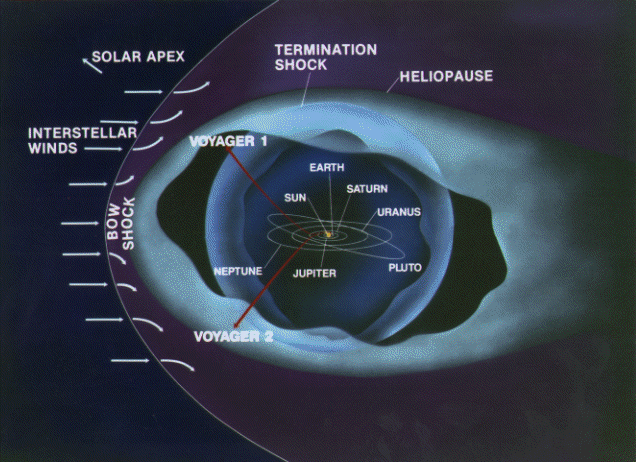
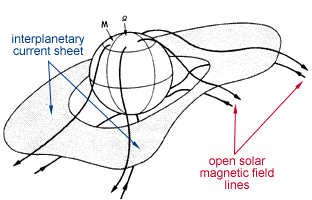
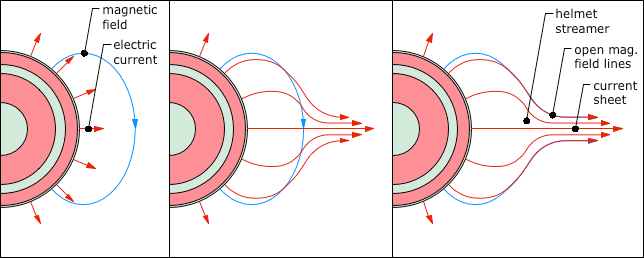
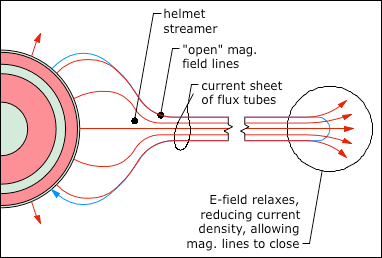
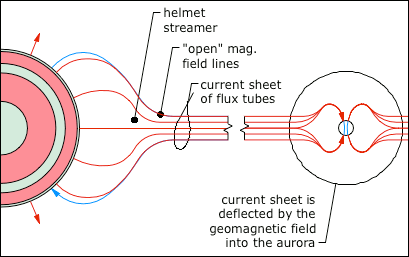
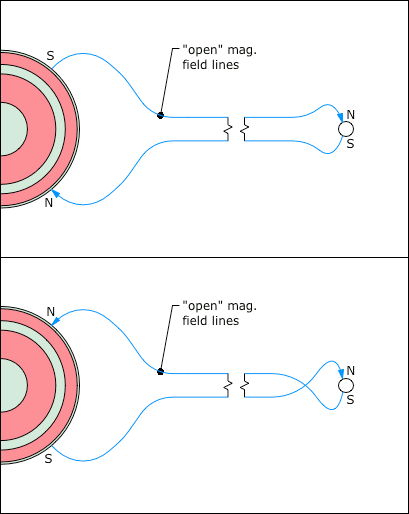
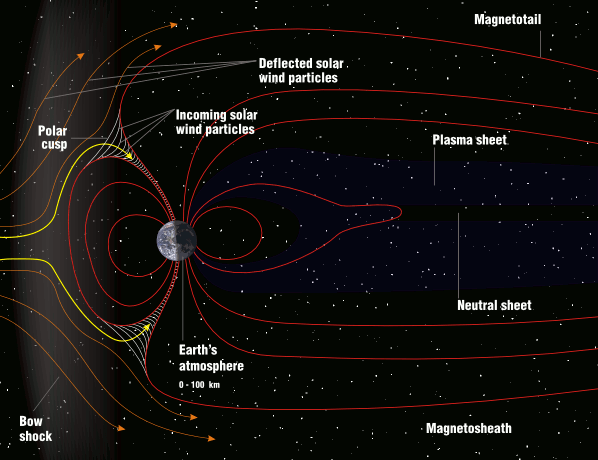
© Charles Chandler

 

Now we should make a direct examination of the larger environment in which all of this is happening. The entire scope of the Sun's influence is known as the heliosphere, with the Sun at the center (of course), and with a radius of something like 1.50 × 10¹⁰ km. Aside from the Sun, the planets, moons, asteroids, and a few comets, the rest of it is a very diffuse plasma known as the interplanetary medium (IPM). (See Figure 1 and Figure 2.) With a total mass of just 3.53 × 10¹⁶ kg, if the IPM were compressed into a solid rock, it would have a radius of just 15 km.¹

 

 

Figure 1. Proton density (i.e., 95% of the constitution of the solar wind) in the interplanetary medium, courtesy Pintéra et al. (2009).

 

 

Figure 2. Same as Figure 1, but with linear scales on both axes, showing that most of the density is near the Sun. At 100 AU, it's 6.25 × 10⁻⁴ protons/cm³.

 

 

The standard model of the IPM is that it is a bubble being blown by the solar wind.² When the bubble runs into the interstellar medium (ISM), the friction brings the solar winds to a stop, forming a "termination shock" that defines the principle extents of the Sun's influence. The interstellar winds, moving at only 23 km/s relative to the Sun, then slowly carry off excess plasma, creating an indistinct coma. (See Figure 3.)

 

 

Figure 3. Standard model of solar and interstellar winds.

 

 

The part of the standard model that isn't correct is the termination shock. The slow solar wind expands at roughly 450 km/s. At that rate, it can traverse the 100 AU from the Sun to the heliopause in just 1.06 years. Surely the solar winds have been blowing for longer than just a year, so shouldn't the heliopause occur at 100 AU, times the number of years the solar winds have been blowing? Or if the ISM is forcing a hard stop, there should be a build-up of matter in the heliopause, equal to the existing density, times the number of years the solar winds have been blowing. If the Sun has been burning for a billion years, the heliopause should be a billion times thicker. But such a build-up of density in the heliopause doesn't exist, as data from Voyager I have shown. Rather, the density is greater beyond the heliopause,³ because the ISM is cooler and denser than the heliosphere, while inside the heliopause, as determined by chemical composition, magnetic fields, etc., the density follows the rule in Figure 1.

 

Another form of analysis begs the same exact question — the total mass of the IPM is just 3.53 × 10¹⁶ kg, and with the mass of the solar wind being 3.15 × 10¹⁶ kg/yr,^4:409,5 the solar wind should be able to populate the IPM to its current density in just 1.21 years. So if the Sun has been burning longer than that, where are all of the particles from years gone by? The interstellar winds, moving at only 23 km/s, won't be able to remove material being supplied by the solar wind at 450 km/s.

 

So where does all of the mass in the solar wind go, if it isn't being whisked away by the interstellar winds, and if it isn't building up in a termination shock at the heliopause? It actually seems to be raining back down on the Sun.^6,7 It's tough to see in the blinding light of charge streams excited to greater than 1 MK in the corona, but once neutralized, particles are free to fall back to the Sun due to the force of gravity, as long as they can stay out of the helmet streamers. In other words, the wind pressure isn't the same in all directions, and while the highly energetic outflow is easy to see, there is an equal-but-opposite inflow that gently recycles neutralized matter. Most of the density in the IPM is very near the Sun, as we can see in Figure 2, and which is due simply to the Sun's 274 m/s² gravitational acceleration. So that's the 3.15 × 10¹⁶ kg/yr making its way back to the Sun.

 

Away from the Sun, the boundary between the IPM and the ISM actually seems to be somewhat less dramatic of a transition than had been expected — there is some turbulence in the heliopause, and the magnetic fields flip every time the wind changes direction. But there is no termination shock. The IPM is hotter, and as a consequence it's less dense, while the ISM is cooler and more dense. Still, the ideal gas laws show that both are at roughly the same pressure (i.e., ~10⁻²¹ pascals). The IPM is a little less dense than it should be, but it also has a slight positive charge, meaning that electrostatic repulsion contributes to the hydrostatic pressure. Thus the IPM and the ISM are in equilibrium, just on the basis of temperature and charge, and without the need for any wind pressure to help maintain the bubble.

 

The positive charge in the IPM begins with the ejection of +ions in CMEs. But at the heliopause, there appears to be another mechanism that increases the positive charge in the IPM. Recent research has demonstrated that when neutral interstellar atoms impinge on the heliosphere, the electrons are stripped off in particle collisions, while the +ions continue into the IPM due to their greater momenta.^8,9 Electrostatic repulsion within the IPM then distributes the positive charges. So when CMEs eject +ions out into the IPM, they are simply adding to an existing positive charge there, and the electrons flowing out of the Sun to re-establish charge equilibrium are attracted to the combined positive charge.

 

Now we have the general context in which to fully understand the behavior of the electron streams coming out of the Sun. While CMEs are discrete events, the equal-but-opposite drift of electrons in response to the charge imbalance is a steady stream. Why don't the electrons respond instantaneously? First, the source of the electrons is a negative layer that is 20 Mm below the surface, so there is resistance to the flow of a current that regulates it. Second, the +ions in a CME, once away from the Sun, are quickly dispersed by their repulsion from each other, leaving just a little contribution to a broadly distributed field, instead of a stronger localized field. Third, the electric lines of force repel each other, further distributing the field. And lastly, the electrons are sitting on a current divider. They are at once attracted to an underlying layer of positive charge, and to the positive charge in the IPM, and a shift in that balance creates only a slight (but sustained) increase in voltage. This creates a sustained electron drift, even if the e.m.f. is episodic, analogous to a relatively steady flow through a dam's spillway, even if rainfall in the catchment area isn't steady, and the water level goes up and down quite a bit. Once the solar winds are liberated from the Sun's gravity and accelerated to 450 km/s, there is nothing to stop them until they reach the heliopause, though the density thins by the inverse square law due to the radial expansion. (See Figure 1.)

 

Figure 4. Heliospheric current sheet, courtesy SWRI.

Next, the heliospheric current sheet (HCS) should be considered. (See Figure 4.) Here we have a fair amount of data, but the standard interpretation makes little sense. Beginning at roughly 1.5 R_⊙, there is a thin sheet of electric current propagating outward from the Sun. The total current at 1 AU has been estimated at 3.00 × 10⁹ A.¹⁰ In the present model, we can easily accept that there is a current, but it's quite low compared to 2.93 × 10¹⁵ A estimated in the Conversions section. Yet this doesn't mean that something is wrong. CMEs expel +ions, motivating an outward electron drift. Once away from the Sun, the electrons are also attracted to the net positive charge in the IPM. So the electrons are driven by the electric force, and the +ions are driven by CMEs, hydrostatic pressure, and electron drag. At some point away from the Sun, the electrons will have caught up with the +ions, meaning no more current. Closer to the Sun, the electrons are still moving faster, registering as a negative current away from the Sun. Since the solar wind appears to still be accelerating at 1 AU,^{11,12,13:9:12} it makes sense that there is still some current, while only directly at the surface of the Sun would we expect the full 2.93 × 10¹⁵ A.

 

The HCS is ridiculously thin, being roughly 10 Mm near the orbit of the Earth, which is thinner than the diameter of the Earth itself. What could keep a current like this organized? The standard model answers this with a riddle. While it is a fundamental law that magnets are always dipoles, astronomers maintain that the Sun has "open magnetic field lines" (or "magnetic flux tubes" as they are sometimes called) that project outward, and the HCS is sandwiched between "flux tubes" of opposite polarity. (See Figure 4.) So what's a "flux tube"? And what binds them together so that they can exert some sort of force on the HCS?

 

To sort this out, we have to start back at the Sun. Figure 5 shows a progression of interactions that ultimately produce the helmet streamers, the open field lines, and the HCS.

 

In the first panel, the electron drift away from the Sun is shown radiating in all directions, along with the typical magnetic field (during the quiet phase).

 

The second panel shows the effect of the magnetic field on the electron drift — the current is deflected in the direction of the B-field, which converges toward the equatorial plane. Nearing the point of convergence, electrostatic repulsion between the electron streams deflects them outward, once again responding only to the attraction to +ions in the heliosphere.

 

The third panel shows the final result, where the current is not only affected by the solar B-field, but modulates it as well. As a field-aligned current, the particles develop a spin. In the gradual transition from the solenoidal back to the radial path at the tips of the helmet streamers, the particles retain their angular momenta, and continue to generate their own magnetic fields. While the solenoidal field deflects the particles into field-aligned currents, it is also true that as the particles are pulled more and more away from the solenoidal form, the B-fields are deflected in the direction of the electron stream. This ultimately resolves into spinning particles streaming out into space, with axial B-fields inside Birkeland currents that have split the solenoid into "open field lines."

 

 

Figure 5. The emergence of helmet streamers and the heliospheric current sheet from a radial current and a toroidal magnetic field.

 

 

This explains the broad base of the helmet streamer, the narrow tip, the "open field lines" in the Birkeland currents, and to some extent, the current sheet in the middle of it all. But it also positions us for a new insight into the true nature of the current sheet. In the standard model, the "magnetic flux tubes" do not have associated electric currents, which is odd because only electric currents can generate magnetic fields. Then, there's the current sheet, which strangely doesn't have an associated magnetic field. The two riddles answer each other. The electric current that generates the magnetic fields in the "flux tubes" is the current sheet itself. Figuratively speaking, if we look closely at the "sheet," we find that it is made of threads, and the threads are Birkeland currents. So it's not that the oddly non-magnetic current is sandwiched between the oddly non-electric magnetic tubes, but rather, that the current through the many tubes constitutes the HCS.

 

Figure 6. Section through "magnetic flux tubes", courtesy Joseph Borovsky.

Figure 7. Closing magnetic field lines.

Figure 8. The Earth's magnetic field does the same thing to the HCS as the Sun's.

Now we can zoom in, and take a close look at the tubes that make up the sheet. Recent research found that the width of the tubes near the Sun corresponds to the width of granules (i.e., ~1 Mm).^14:1 (See Figure 6.) This is consistent with the present model, in which there is a steady drift of electrons away from the Sun. Electron drag creates the updrafts in the center of the granules, while the +ions in the downdrafts around the outsides have to fight against electron drag. As a consequence, electrons emerging from the center of the granules will be traveling faster, having lost less speed to collisions with +ions. Once out of the photosphere, these electron streams accelerate, and become subject to the Sun's magnetic field, which sends the electrons into rotation around magnetic lines of force (i.e., as Birkeland currents). The gyroradii of the electrons (at 500 MeV) is comparable to the radius of the solar granules.^14:21 And neighboring Birkeland currents refuse to merge, since they generate magnetic fields that repel each other. So it makes sense that the flux tubes start out corresponding 1:1 with granules.

 

So what ultimately becomes of these "open field lines", which have to close sooner or later? All other factors being the same, at some point in the heliosphere, the electrons will catch up to the +ions, and thereafter there will be no net current. This means no more magnetomotive force, and the magnetic field lines will be free to close. (See Figure 7.) Since Birkeland currents of both magnetic polarities are projecting outward, the nearest closing point for their magnetic fields will be each other. Hence the magnetic field lines form a continuous loop, starting inside the Sun, following Birkeland currents out into the heliosphere, and returning to the Sun through similar Birkeland currents of the opposite polarity.

 

But things will be different if the HCS encounters a planetary magnetic field, such as the Earth's. At 1 AU, the density of the magnetic field in the tubes is only 10⁻⁹ teslas, while the Earth's field is 5.00 × 10⁻⁵ teslas, which is easily strong enough to force the HCS into geomagnetic alignment. (See Figure 8.) Since the HCS contains B-fields of both polarities, these will be sorted by the geomagnetic field, with one polarity getting directed to the North Pole, and the other to the South Pole.¹⁵

 

Of course, the Sun's magnetic polarity will only match the Earth's during every other cycle, since it flips every 11.2 years. If the Polaris-facing hemisphere of the Sun has a south polarity, its flux tubes can feed directly into the North Pole of the Earth, as in the upper panel of Figure 9. But in the next solar cycle, the Sun's polarity will be opposite. When the HCS reaches the Earth, and the Birkeland currents are sorted on the basis of the polarity of their axial fields, all of the tubes will have to weave their way past each other, as depicted in the lower panel.¹⁶

 

Figure 10 shows a more detailed view of the capture of the HCS by the geomagnetic field. Some of the solar wind flows around the Earth, if it is far enough away that the Earth's field is too weak and/or the hydrostatic pressure is too great for capture. And some of the Earth's lines of force are captured by the solar wind, and "opened" as the Birkeland currents continue deeper into space.

 

 

Figure 9. Alignment of magnetic hemispheres.

Figure 10. Geosphere, credit Aaron Kaase, courtesy NASA.

 

 

This explains why the aurorae are more brilliant when the solar field is "southward" near the Earth, meaning that its field lines feed directly into the Earth without crossing (as in the upper panel). If the flux tubes don't have to cross each other, they won't lose any energy in so doing.

 

Figure 11. Flux tubes in the heliospheric current sheet, courtesy Joseph Borovsky.

That the flux tubes can cross each other is evidenced by data from ACE, as in Figure 11.¹⁴ The general direction follows the Parker Spiral, but locally, individual tubes pick their own paths. Clearly there is an external force that is acting on the tubes, to overpower their momenta, and the hydrostatic pressure, which would prefer an homogenous body of plasma with no internal disruptions. And the only external force is the Earth's magnetic field. So these are flux tubes getting geomagnetically aligned.

 

Figure 12. Parker's Spiral

The undulations in the HCS, due to asymmetry in the helmet streamers, are typically thought to ignore the planets, as in Figure 12. But the Earth's magnetic field dominates a volume far bigger than itself, and thus should be capable of trapping the HCS in spite of the undulations. And once aligned, it should stay aligned. So the actual Parker's Spiral should show a perturbation around the Earth. Beyond 10 AU, the electrons in the HCS have caught up to the +ions, and thus we should expect the HCS to fall apart. But there should still be a perturbation due to Jupiter's strong magnetic field.

 

This is consistent with the fact that there is always a measurable aurora, at the poles of the Earth as well as Jupiter. If the HCS undulated freely, we would only see the aurora when the HCS happened to be passing through the ecliptic plane. But if the HCS is captured by planetary magnetic fields, the aurora will always be visible.

 

To produce the observed radiation in the aurora, the particles have to be accelerated from the speed of the solar wind (i.e., less than 800 km/s) up to 60,000 km/s,¹⁷ despite the increasing density of the atmosphere. The motivating forces are both electric and magnetic. We know that the electrons in the solar wind are still traveling faster than the +ions at 1 AU. If this differentiation is not maintained, electrons and +ions in the solar wind will recombine, and thereafter not be influenced by the geomagnetic field. So the electric force has to enhance the electron velocity, meaning that the Earth would have to be showing a positive charge. The Earth is actually net neutral, but the solid/liquid surface is negative, while the atmosphere is positive. Due to the inverse square law, a negative test charge in space will be attracted to the Earth, because the positive charge is closer.¹⁸ So the E-field is going in the right direction.

 

This effect, of the attraction of negative charges to a positive outer layer, will only carry the electrons so far — at some point in the atmosphere, the field flips. Starting at the surface, which is negative, any +ions in the lower atmosphere will be pulled down. So that's a downward conventional current. But with increasing distance from the surface, that attraction decreases, first because of distance (and the inverse square law), and second because of repulsion from +ions below them. At roughly 50 km above the surface, the E-field starts to weaken,¹⁹ and somewhat higher, it drops to nothing. Still higher, the field inverts, where it isn't +ions that are being pulled down, but electrons. Thus it becomes an upward conventional current, or downward flow of electrons. This is interesting because the aurora stops somewhat abruptly, at about 80 km above the surface. Above that level, electrons are still being accelerated and +ions decelerated, maintaining the charge separation. But at 80 km, the field flips, which removes the speed difference, and enables charge recombination, with the associated photon emission. Once the charges have been neutralized, the particles are no longer controlled by the geomagnetic field, and are invisibly dispersed. So the base of the aurorae is defined by the structure of the electric fields.

 

 

Figure 13. Aurora Borealis, courtesy NASA.

 

 

The magnetic acceleration comes from the convergence of magnetic lines of force, starting at the polar cusp, and continuing to near the surface, where the lines become nearly parallel, adding little to the velocity of the Birkeland currents.

 

With electrons traveling faster than +ions, they would seem to deliver a net negative charge to the Earth, and at both poles. Certainly this cannot continue forever without neutralizing all of the +ions in the atmosphere, thereby eliminating the attraction of electrons. The mechanism that sustains the atmospheric charge (i.e., electron degeneracy pressure inside the Earth creating charged double-layers) is detailed in the section on the planetary sciences, but in the present context, it is sufficient to say that the surface of the Earth is negatively charged for internal reasons, and it repels surplus electrons, which then drift outward from the equatorial regions. They cannot escape at the poles, since this would have them traveling parallel to magnetic field lines, which would turn them into Birkeland currents, but which do not flow against diverging lines of force. So the electrons can only escape nearer the equatorial plane, though their motion is braked by traveling perpendicular to the magnetic field. This creates a concentration of charged particles in the Van Allen belts. From there, the electrons can leak back into the solar wind, especially on the leeward side. And once again, the motion of electrons in a toroidal magnetic field both flattens them into a sheet, and opens the magnetic field lines in the magnetotail, which is the equivalent of a helmet streamer in the solar corona.

 

Calculations