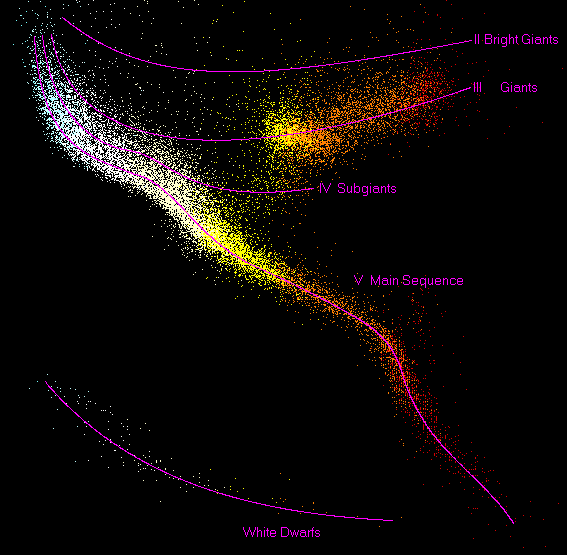
© Charles Chandler

 

Now we can see if the model that explains The Sun applies to other stars as well.

 

We had previously examined the "exotic" stars, such as Quasars, and considered the properties of a "natural tokamak" (NT) as the explanation. Then we saw that our Sun is not like that. Its average magnetic field is weak, and magnetism is not the organizing principle as it is in a tokamak. Rather, the Sun is held together by electrostatic forces between current-free double-layers (CFDLs), created by pressure charging. In that framework, a highly detailed description of the Sun became possible.

 

Interestingly, most stars seem not to be tokamaks either, as they have weak magnetic fields, and they emit very few x-rays and gamma rays. So we should like to see if the CFDL model generalizes to explain all of these "non-exotic" stars.

 

Figure 1. Hertzsprung-Russell diagram.

The best place to start is with the Hertzsprung-Russell diagram, which sorts out the stars on the basis of luminosity (on the vertical axis) per color (on the horizontal axis).¹ (See Figure 1.) This reveals some distinctive patterns. 90% of all stars are in the "main sequence," from bright, blue stars at the upper left, to dim, red stars at the lower right. Our yellow Sun is in the middle of this sequence. Other patterns include the cluster in the upper right known as the red giants, and a band of stars at the lower left known as the white dwarfs.

 

As is always the case in physics, distinctive patterns are evidence of forces, and the main sequence is definitely distinctive. So what are the forces responsible for this luminosity/color relationship?

 

First we can observe that the spectra in all of the main sequence stars are blackbody curves, like our Sun. But as noted in the BB Radiation section, the standard model of the Sun fails to explain solar blackbody radiation. In consideration of the full range of stars in the main sequence, this failure gets even worse. It's unlikely enough that gamma rays (supposedly) generated in the Sun's core could get transformed into a smooth 5525 K BB curve just by a chance combination of elements. It would be far more chancy for the color temperature to vary continuously, from 6400 K when viewed normal to the surface, to 4600 K at the limb, since this would require a stratification of many more chance combinations of elements. And that's assuming that the photosphere could support such stratification, but it's too well mixed for that. So the standard model of solar BB radiation is already untenable, because it tries to make a rare coincidence happen as a rule. Then we find that 90% of all stars issue BB radiation, putting even more pressure on the rare-makes-rule problem. If that weren't enough, we can observe stars whose luminosity and color vary, sometimes in as little as a couple of days, such as the Cepheids.² Since the pseudo-BB curve in the standard model requires a specific combination of elements, variable BB curves require varying combinations of elements. For the elemental abundances to vary that fast is hard to believe. For them to cycle repeatedly through the same series of combinations, just by chance, is even harder to believe. But if there were that much fusion and fission happening near the surface of the Cepheids (which the standard model doesn't allow), the abundances of elemental by-products would obey ratios well-known to nuclear physicists, and which have nothing to do with the requirements for pseudo-BB curves. And of course the fusion & fission near the surface would make the stars prodigious gamma ray emitters, leaving the actual BB curves unexplained.

 

Aside from such statistical impossibilities, there are more mechanical problems. In the standard model, bright blue stars are more massive, and therefore have hydrogen fusion furnaces that are more prolific, thus the greater luminosity. But that doesn't explain the color. A more massive star would require photons to travel through much more plasma to get out to the photosphere. If the frequency is getting stepped down in this process,³ the photons that escape should be redder, not bluer. As a rough metaphor, we can observe that at sunset, the light is redder. The temperature at the surface of the Sun hasn't changed, but the light is passing through more of our atmosphere, which scatters the blue frequencies. Of course, the scattering doesn't redshift the BB curve — it just absorbs a bigger chunk of it in the higher frequencies. But in the standard model of BB radiation, the atmosphere should redshift the whole curve. After all, the Earth's atmosphere is far thicker than the plasma near the surface of the Sun in the standard model. Similarly, the great depth of a giant star should redshift the photons, if that's what is actually happening. Thus in the standard model of pseudo-BB curves, red giants and white dwarfs make sense, but blue giants and red dwarfs (i.e., the main sequence) do not.

 

The CFDL model incorporates a more plausible mechanism for BB radiation, as the oscillations of charged particles in a supercritical fluid. This doesn't dictate a specific temperature, nor that it be static. "Hotter" BB temperatures are produced by more densely packed matter, which shortens the mean free path of vibrating atoms, thereby increasing the frequency. Gravity cannot compact plasma to such densities at the outer edge of a star, so stellar BB radiation can only be evidence of an electric field that compresses the outer layer, and "hotter" stars simply have stronger near-surface electric fields.*¹⁴⁸⁷⁷

 

Figure 2. Comparison of sizes in the standard stellar model, with (top to bottom) Bellatrix, Algol B, the Sun, a red dwarf, and two planets.

© 2007 Paul Stansifer

Note that a shorter mean free path results in both higher frequency photons, and more of them, since a new photon is issued with each oscillation. Thus the "hotter" star is bluer and brighter. If the near-surface electric field relaxes, the photons will be redder and dimmer. But it will take more than that to explain the actual difference in luminosity between bright blue and dim red stars. According to the Stefan-Boltzmann Law, the luminosity of a BB emitter varies with the fourth power of the temperature. So Bellatrix, a blue star in the Orion constellation, and with a surface temperature of 22,000 K, should be 181 times brighter than the Sun, whose surface temperature is 6,000 K. Bellatrix is actually 6,400 times brighter, or 35 times brighter than it's supposed to be. The standard model makes up the difference by increasing the surface area of Bellatrix by a factor of 35. (See Figure 2.) But this causes problems — with a higher temperature comes greater hydrostatic pressure, and at the same mass, the star would expand to a lower density, which would mean weaker gravity. More hydrostatic pressure and less gravity would throw the star out of hydrostatic equilibrium, and the star would fall apart. To keep the star organized, the standard model has no choice but to increase the mass, to provide the gravity to offset the increased hydrostatic pressure. So Bellatrix gets assigned 8.4 solar masses. The problem with that is that there are limits to how high the temperatures and pressures can get without initiating a runaway thermonuclear explosion (i.e., a Type 1a supernova). If the conditions in the core of the Sun are sufficient for sustained hydrogen fusion, the conditions inside Bellatrix are easily sufficient for a supernova.

 

Other lines of evidence confirm the limits set by supernova theory. For example, the masses of stars when they first form are relatively consistent, with most stars beginning at roughly 1/3 the mass of the Sun.^4,5,6,7 Since there is no reason to believe that anything regulates the size of the dusty plasmas that implode into stars, we'd expect a random distribution. The statistical preference for ~1/3 M_☉ is then evidence of limits imposed by the newborn stars themselves. The upper limit would be 1.4 M_☉,⁸ before nuclear physics intervenes. Perhaps the lower limit is how much matter needs to be present to set up the CFDLs to hold it all together. Regardless, if 1.4 M_☉ is the upper limit, 8+ M_☉ is way out of range.

 

If not with additional mass, how can we account for Bellatrix's 35x luminosity? The answer might be that the Stefan-Boltzmann Law is naïve. It emerged in the late 1800s from the study of solids that emit BB radiation (especially graphite),^9,10 as an extension of the works of Balfour Stewart¹¹ and Gustav Kirchhoff.¹² They didn't have the experimental technology to directly measure plasmas, and it wasn't known until far more recently that supercritical fluids emit BB radiation.^13,14 So it might be true that the luminosity from a solid surface varies directly with the fourth power of the temperature, but plasmas don't have a surface in the same sense, and the Stefan-Boltzman Law might need another factor for the effective depth of the radiator, where the total power output would be the surface times the depth. Then we might get 35 times more photons from a plasma at a given temperature than we would from a solid surface, because we're getting photons out of a volume of matter, not just off of a surface. The difference between Bellatrix and the Sun is then a matter of the opacity of the plasma in differing electric fields.

 

Next we should consider what happens as a star ages. The standard model asserts that stars stay on the main sequence pretty much where they were born, until they eventually decay into either red giants or white dwarfs, but it's interesting to consider the possibility that the stars actually shift down through the main sequence with age.¹⁵ So a bright blue star might eventually evolve into a dim red star, as a simple consequence of radiative heat loss. As the star cools, the atoms vibrate slower, releasing fewer photons, and at lower frequencies. Cooler matter is also less ionized, making it less susceptible to electric fields, which means that the CFDLs won't be compacted as much. Thus the mean free path between ions increases, which also decreases the frequency of the photons. Eventually, the star will have cooled to the point that the hydrogen and helium will no longer be ionized, and the electric fields will no longer be able to hold onto them. So the lighter elements will drift off, exposing the heavy-element core & atmosphere. The core will eventually freeze over, and then we'll call it a planet.¹⁵ (See Light Curves for the calculations.)

 

Thinking that stars evolve along the main sequence makes sense of another fact, this time concerning galactic evolution. The bright blue stars on the leading edges of spiral arms are young, while the yellow-red stars in the elliptical bulges are old. All of these stars are on the main sequence. So why are young stars typically blue, and old stars yellow or red? This is expected if they evolve from blue to red with time.

 

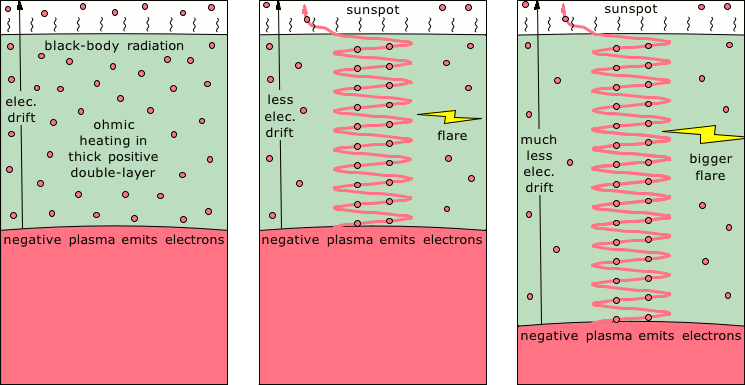
Table 1. Milky Way Abundances Element Percent Hydrogen 73.97 Helium 24.02 Oxygen 1.04 Carbon 0.46 Neon 0.13 Iron 0.11 Nitrogen 0.10 Silicon 0.07 Magnesium 0.06 Sulfur 0.04

This also answers another troubling question in stellar theory. The Elements section established that only 66% of the Sun's volume is hydrogen and helium, while 34% of it is heavier elements (iron, nickel, platinum, & osmium). This stands in stark contrast to typical abundances elsewhere, such as throughout the Milky Way, as shown in Table 1. So how did the Sun come upon such great abundances of heavier elements? There are two possibilities. First, the Sun could have condensed from a dusty plasma with 34% being heavier elements. But then we'd expect the heliosphere and the nearby interstellar medium to be 34% heavier elements, which is not the case. Second, the Sun might have once been a much hotter star, capable of fusing heavier elements.

 

Note that the evolution down the main sequence isn't a straight line — there are two humps, one at the transition from blue to yellow stars, and the other between yellow and red stars. Since the standard model doesn't address this, we should look to the CFDL model for an answer. Figure 3 shows the proposed layers within the Sun. As it continues to cool, the bulk ionization will relax, reducing the electric force between charged double-layers. This will allow the star to expand. The reduced density will relax the internal pressure, shifting the thresholds for charge separation by electron degeneracy pressure (EDP) downward. In other words, such thresholds occur at isobars, and if the pressure is relaxed, we have to go deeper to find the same isobars. The significance is that the near-surface conditions will change — the topmost positive layer will get deeper, because its bottom has shifted downward, and because its top isn't as firmly bound. The greater mean free path will yield redder photons. And note that this is a shift in frequency in addition to the shift from the reduced temperature. So a little bit of temperature difference results in a lot of reddening, and not a lot of decrease in luminosity (since that varies just with the temperature). Hence we get an explanation for the flatter stretch in the main sequence, before the yellow-to-red hump.

 

Thickening of the topmost positive layer also has implications for stellar flaring. We saw in the CMEs section that a deeper photosphere increases the chances of solar flares. All other factors being the same, the electron drift out of the Sun is evenly distributed, because the dominant force is the repulsion between the electrons. But as the resistance increases with the thickness of the photosphere, the distribution becomes unstable, and can rather favor tunneling through the resistance in discrete channels, which resolve into sunspots, and which set the stage for flares. So if the photosphere gets thicker, because the underlying negative layer is shifting deeper into the Sun, flares will occur more frequently, and more violently. And these are precisely the characteristics of stars as they approach the red dwarf stage, where flares can sometimes double the luminosity of the star in a matter of minutes. (See Figure 4.)

 

 

Figure 4. The effect of the thickness of the topmost layer on the radiation emitted by the star. In the first panel, a weak electron drift is well distributed by repulsion between electrons. In the second panel, a somewhat faster drift starts to tunnel through the resistance as a sunspot. In the third panel, with an even thicker layer of resistance, a sustained electric current discharges the potential, and the electron drift outside of the tunnel is much weaker. The result is a dimmer star, but with more dramatic flares.

 

 

At the same time, this explains the steep section of the hump in the main sequence, entering the red dwarf stage. As the photosphere thickens, the electrical resistance continues to increase, eventually choking the electric current that heats the photosphere. What little electric current persists flows mainly through discrete channels in star spots, which have little effect on the overall temperature of the photosphere. Thus the reduction in ohmic heating and the increase in flares are coupled, and the star's luminosity drops rapidly, despite episodic brightenings.

 

Other distinctive patterns in the Hertzsprung-Russell diagram include the cluster of red giants at the upper center, and the white dwarfs at the lower left.

 

The white dwarfs are strange stars indeed. They are (supposedly) incredibly dense, where the mass of the Sun could be packed into the volume of the Earth. (That's 333,000 times more dense than the Sun!) And the surface temperatures can exceed 150,000 K.¹⁶ So something has gone seriously wrong with the ideal gas laws, because the hydrostatic pressure shouldn't have allowed condensed matter with such thermal energy. White dwarfs also have extremely powerful magnetic fields (as high as 300 million Gauss!¹⁷). The angular velocities necessary to generate such fields will add powerful centrifugal forces to the already-overpowering hydrostatic pressures. To offset these forces and keep the stars organized, the standard model has to assert densities not allowed by atomic theory, to get the gravity it needs. Past that point, nothing makes sense. How does the angular velocity of degenerate matter give rise to a magnetic field? Or issue photons for that matter? All of the answers are as unrealistic as the premise, since atomic theory has already been abandoned.

 

Are white dwarfs actually outside the range of atomic theory? Hardly — tokamaks generate extreme temperatures with powerful magnetic fields. And they don't need impossible densities to do so. Thus the "natural tokamak" (NT) model is more realistic, putting white dwarfs in the same category as quasars and the central stars in planetary nebulae.

 

The "red giants" might not be stars at all, but just aspects of NTs that the standard model cannot reconcile with its exotic star theory. For example, the standard model has Mira (mentioned in the Supernovae section) as a binary system composed of a white dwarf and a red giant. And yet in UV light, both members of the system are nearly identical, which is not at all the expectation for such dramatically different star types. (See Figure 5.) This makes a lot more sense if both "objects" are just the limbs of a toroidal plasmoid, where the UV radiation is coming from the extreme temperatures near the tokamak, and the BB radiation is coming from a thick atmosphere around the outside, which was ejected during the formation of the central star. Red giants are also frequently identified in the cores of planetary nebulae, which clearly have NT properties.

 

In conclusion, we have two stellar models: the NT model (for the exotic stars), and the CFDL model (for main sequence stars). And while conventional astronomy asserts any normal star, such as our Sun, could collapse into an exotic star, wherein the determining factor is simply the amount of mass, the present model asserts that the difference between a normal and an exotic star is relativistic angular velocity. Main sequence stars don't have this, and wouldn't have it even if they did collapse (if that were even possible). So main sequence stars evolve into brown dwarfs, and ultimately, into planets. The exotic stars likewise cool with time, and get redder, but they fall apart when the angular velocities can no longer sustain the organizing magnetic field. So there are no dark tokamak stars.

 

The General Theory of Stellar Metamorphosis

Transparency of the Sun and Similarities to Organic Material

Red Giants/ Giant Stars simple miscalculation of distance using unreliable parallax.

Notes on BB Radiation