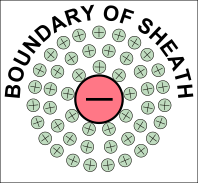
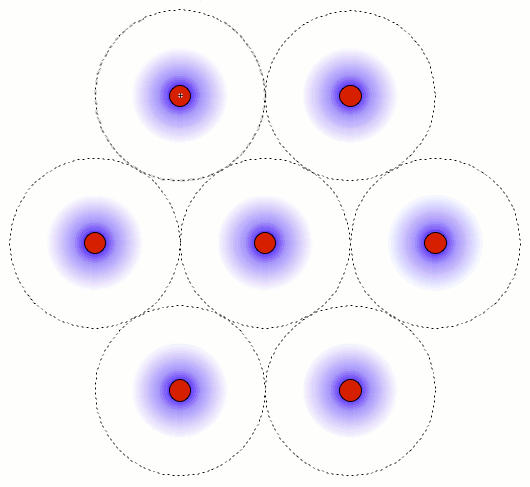
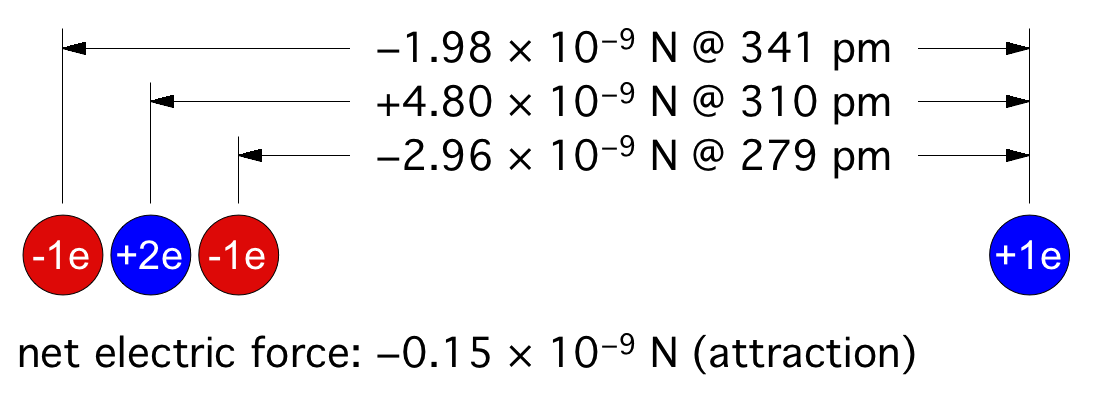© Charles Chandler

 

We should start at the beginning, which means that we need to understand how celestial bodies condensed from dusty plasmas in the first place.

 

In 1687, Sir Isaac Newton published his Universal Law of Gravitation,¹ which identified the force that keeps planets in orbit around the Sun, and moons in orbit around the planets. But in his day, the prevailing opinion was that these objects were created, in situ, less than 10,000 years ago. Only later did people start considering the possibility that celestial bodies were somehow formed, and over much longer periods of time.²

 

Figure 1. Keyhole Nebula.

By the 1800s, improved telescopes were detecting dust clouds in space. And sometimes, there were voids in dust clouds, with new stars in the centers of the voids, such as the star in the center of Figure 1.^3:33~35 The conclusion was that the missing dust had formed the star when it collapsed under its own weight. At the same time, scientists knew that hydrostatic pressure in the cloud would oppose the gravitational collapse. So they supposed that there was a threshold that had to be crossed to enable the collapse — if the hydrostatic pressure was weak, and/or if the gravity was strong, the collapse would begin. As the density of the cloud increased in the center, the force of gravity would get stronger, further consolidating the matter. In a sufficiently dense cloud, gravity would overpower hydrostatic pressure, packing all of the matter into a star. This came to be known as the Jeans Instability, and it has become the standard model of star formation, now so deeply entrenched as to be difficult to challenge.

 

Yet it is fundamentally flawed. In Newtonian mechanics, there is no gravitational instability. Rather, there is a hydrostatic equilibrium — the opposite of an instability. It is true that gravity exerts an inward force, and as matter gets pulled inward, it gets more dense, which makes the gravity field even stronger. And gravity obeys the inverse square law, which means that it increases exponentially as the volume decreases. Nevertheless, there is an opposing force — the hydrostatic pressure increases as a direct function of the decreasing volume (i.e., Boyle's Law), and this force actually increases faster than the gravity, leading invariably to an equilibrium, beyond which gravity is weaker than pressure. At that point, the gravitational compression stops. This is why, for example, the Earth's atmosphere doesn't collapse under its own weight, despite having a higher concentration of heavy elements than is typical in space, making it more subject to the force of gravity, and despite the Earth providing a lot more gravity than a dusty plasma provides for itself, and despite being much cooler than a dusty plasma compressed to the same density,⁴ — the hydrostatic equilibrium has already been achieved, and the gravitational collapse doesn't happen.

 

Knowing this, scientists have concluded that something must be removing the hydrostatic pressure. So they suppose that as the compression raises the temperature, eventually the matter gets hot enough to start issuing EM radiation (i.e., photons). If the photons escape the dusty plasma and proceed on out into space, this represents a net energy loss for the dusty plasma, and it will have cooled itself. At a lower temperature, there will be less hydrostatic pressure, enabling more compression. But photons are an extremely slow heat loss mechanism, especially at first, when the difference in temperature between the dusty plasma and its environment is slight. And if somehow the collapse continues, eventually the cloud will become dense enough to absorb all of its own radiation, making the energy loss via photons even less efficient.

 

Ongoing studies of stellar nurseries have compounded the problem. It is becoming clear that dusty plasmas ordinarily do not collapse under their own weight (no surprise there), but when two gas clouds collide, especially when two galaxies merge,^5,6,7 or if a gas cloud is impacted by the ejecta from a nearby supernova, a collapse is initiated that ultimately results in the formation of a star. So it's something to do with the collision. In the standard model, the combination of matter from two different sources doubles the mass, and gravity takes over.⁸ But the collision also doubles the hydrostatic pressure, and if the dusty plasmas were already at equilibrium, now there should be too much pressure, resulting in the expansion of the plasma, not the collapse. Furthermore, the velocities in such collisions are in excess of 20 km/s, and the thermalization of such kinetic energies will greatly increase the hydrostatic pressure. This will cause the expansion (or even the explosion) of the gas, which is the opposite of a collapse.

 

Some of the lay literature on the topic suggests that the pressure trough behind a supernova shock front enables condensation within the cloud, the same way an explosion in humid air forces the condensation of water vapor, leading to the gravitational collapse of the cloud. It's true that a shock wave can cause condensation, but that won't lead to a subsequent gravitational collapse of everything that condensed. The gravitational body force on the cloud actually decreases when gases condense, because the distance between particles responsible for the body force increases, and because gravity obeys the inverse square law.

 

Clearly, Newtonian physics just doesn't have an answer for what enables the collapse of dusty plasmas into stars, so we'll have to look at non-Newtonian forces. There are two of them operative at the macroscopic level: the electric force, and the magnetic force. There is no known configuration of magnetism that could create a body force on a dusty plasma. But there is a way that electricity could do the job. And we know that the electric force is present, because we know that the dusty plasmas are ionized — that's why we call them plasmas. It's just that there is a significance to this that hasn't been previously investigated.

 

Figure 2. Debye cell.

The ionization exists in Debye cells, roughly 1 m in diameter, with a negatively charged dust grain in the center, and with a halo of +ions clinging to it.⁹ (See Figure 2.) The dust grains develop a negative charge because of the difference in mass between electrons and atomic nuclei. At any given temperature above absolute zero, particles are moving about, but free electrons move at least an order of magnitude faster, possessing the same kinetic energy as nuclei, but with a lot less mass. Because of the greater speed of electrons, any dust grain in the vicinity gets bombarded with more electrons than +ions. And those electrons are absorbed into the electron cloud of the dust grain, which can typically host as much as 1 extra electron per million nuclei. The entire electron cloud simply shifts when an extra electron is added, and the attraction to the positively charged atomic nuclei is still stronger than the repulsion between like-charged electrons. The net charge will persist until the +ion that lost its electron impacts the dust grain. If the impact is vigorous, the atom might pick up its lost electron and just bounce off, while a gentle contact might result in the new atom getting captured by covalent bonding. Either way, the rate at which the dust grain is bombarded with free electrons is what maintains the charge separation. The entire cell is net neutral, but the dust grain is negatively charged, surrounded by +ions that have yet to recover their lost electrons.

 

The net neutrality of the entire cell led Irving Langmuir to the conclusion that such cells would not interact electrically with their surroundings. Hence he borrowed the term "plasma" from biology as an analogy for cells that insulate their contents from their neighbors.¹⁰ Interestingly, we have exactly the same set-up (at a much smaller scale) in atoms with their positively charged nuclei and negatively charged electron clouds. The polarity might be opposite, comparing Debye cells to atoms, but the electric force works the same either way, and it's scale independent. So we can borrow from the somewhat larger body of research that has been done on the electric interactions between atoms.

 

Figure 3. Electric forces between a neutrally charged helium atom at left, with 2 electrons as point sources at the K shell radius of 31 pm, and a positive test charge at right, arbitrarily 310 pm from from the helium nucleus, showing a slight net attraction.¹¹ At the same distances, gravity is just 7.77 × 10⁻⁴⁵ N, so it isn't a factor.

Richard Feynman was the first to realize that there is a hidden significance to the electric force's inverse square law that is important in bringing atoms together to make molecules.^{12:ch2:pg2,13,14,15,16,17} He said that it requires ionization, because a positive ion is attracted to a neutrally charged atom. The reason is that the negative charges in the neutral atom's electron cloud get nearer to the distant positive ion. Then if we just look at the effects of the inverse square law, we realize that the near-side electrons exert a greater attraction per elementary charge on the positive ion than the repulsion from the atomic nucleus, and the attraction to the far-side electrons isn't that much less. If we add up all of these +/− forces, we find that the neutral atom shows a slight net negative charge at a distance. (See Figure 3.)

 

This means that any nearby positive ion will be pulled toward the neutral atom, despite the net charge of the whole assembly being positive (ergo the paradoxical "like-likes-like" effect). We should also note that the attraction gets stronger as the positive ion gets nearer to the neutral atom, since the relative proximity of the positive ion to the near-side electrons gets more dramatic. It's also possible (depending on which atomic model is used) that the electrons favor that near side, being attracted to the positive ion. If there is even more negative charge on the near side of the neutral atom, the positive ion will experience an even greater attraction. So the positive ion is pulled toward the neutral atom, to the point of sharing electrons with it, thereby forming a molecule.

 

The corollary is that if both atoms are neutrally charged, they will both be showing a net negative charge at a distance, and they will repel each other. This is why the elements with fully populated outer electron shells (i.e., the noble gases) are the least likely to form molecules — electrostatic repulsion within the shells calls for an equal distribution of electrons, and if the shell is fully populated, there is nowhere for electrons to go if exposed to a negative test charge at a distance, so they stay where they were, and push back. This is also why the elements with the lowest ionization potentials are the best at forming molecules — once one of the atoms gets ionized, the net electric force goes from repulsive to attractive.*¹⁴⁵³²

 

All of this can be applied directly back to Debye cells, if we just flip the charges. Two neutrally charged Debye cells will see a net repulsion, because of the proximity of their +ions, and because of the inverse square law.^18,19,20 (See Figure 4.)

 

 

		← net repulsion →
Figure 4. The sheaths of neighboring Debye cells produce a net repulsion between the cells, because of the inverse square law.

 

 

How much repulsion? For dusty plasmas, the strength of the electric force compared to gravity was calculated. First, a negative dust grain was surrounded by a random distribution of +ions, and with more of the ions nearer the dust grain than further away (i.e., 80 of them within 25% of the overall radius of the cell, 40 of them within 50%, 20 of them within 75%, and another 10 around the outside). That made a total of 150 +ions, so the corresponding charge on the dust grain was set to −150 e. The radius of the entire cell was set to 1 m. (See Figure 5.)

 

 

Figure 5. Particles in the simulated Debye cell, where the nucleus is red, and the 150 randomly distributed +ions are blue.

 

 

To estimate the mass distribution so that the force of gravity could be calculated, the degree of net ionization must be known. It was mentioned earlier that a dust grain can host as much as 1 extra electron per million atoms, but that's a high-end number. A far more conservative estimate would be 1 ion per 10¹⁵ neutral atoms. So the 150 +ions were each assigned a charge of +e, and the mass of a proton times 10¹⁵. The dust grain in the center was assigned a charge of −150 e, and a mass of 150 protons times 10¹⁵. (The masses of the electrons were neglected.) This produced a realistic mass and charge distribution within the Debye cell. Then the net force between neighboring Debye cells could be calculated simply by adding up all of the electrical and gravitational forces between each of the point sources within the cells.

 

To improve the accuracy, the test cell wasn't surrounded by just one layer of neighboring cells, which in a 3D closest packed arrangement would have meant 12 neighbors — another layer was added around the outside, so that the more distant forces would also be included. This produced 56 neighboring cells. (See Figure 6, Figure 7, and Figure 8.)

 

 

HCP closest packed arrangement of 57 spherical Debye cells.

Figure 6. Top view.

Figure 7. Perspective view.

 

 

 

Figure 8. Section view of 7 Debye cells in a closest packed arrangement. Red is negative; blue is positive. The radius of each cell is 1 m. The dust grain in the center was treated as a point source (i.e., with no radius), as were the 150 +ions surrounding it (shown here just as a radial gradient).

 

 

Then the gravitational and electric forces between the particles in the Debye cell at the center, and all of the other 56 Debye cells, were summed.

 

 

Equation 1. Gravity F = Gm1m2/d2 where: F = force (newtons) G = gravitational constant m1 = mass of first object (kilograms) m2 = mass of second object (kilograms) d = distance between centers (meters)

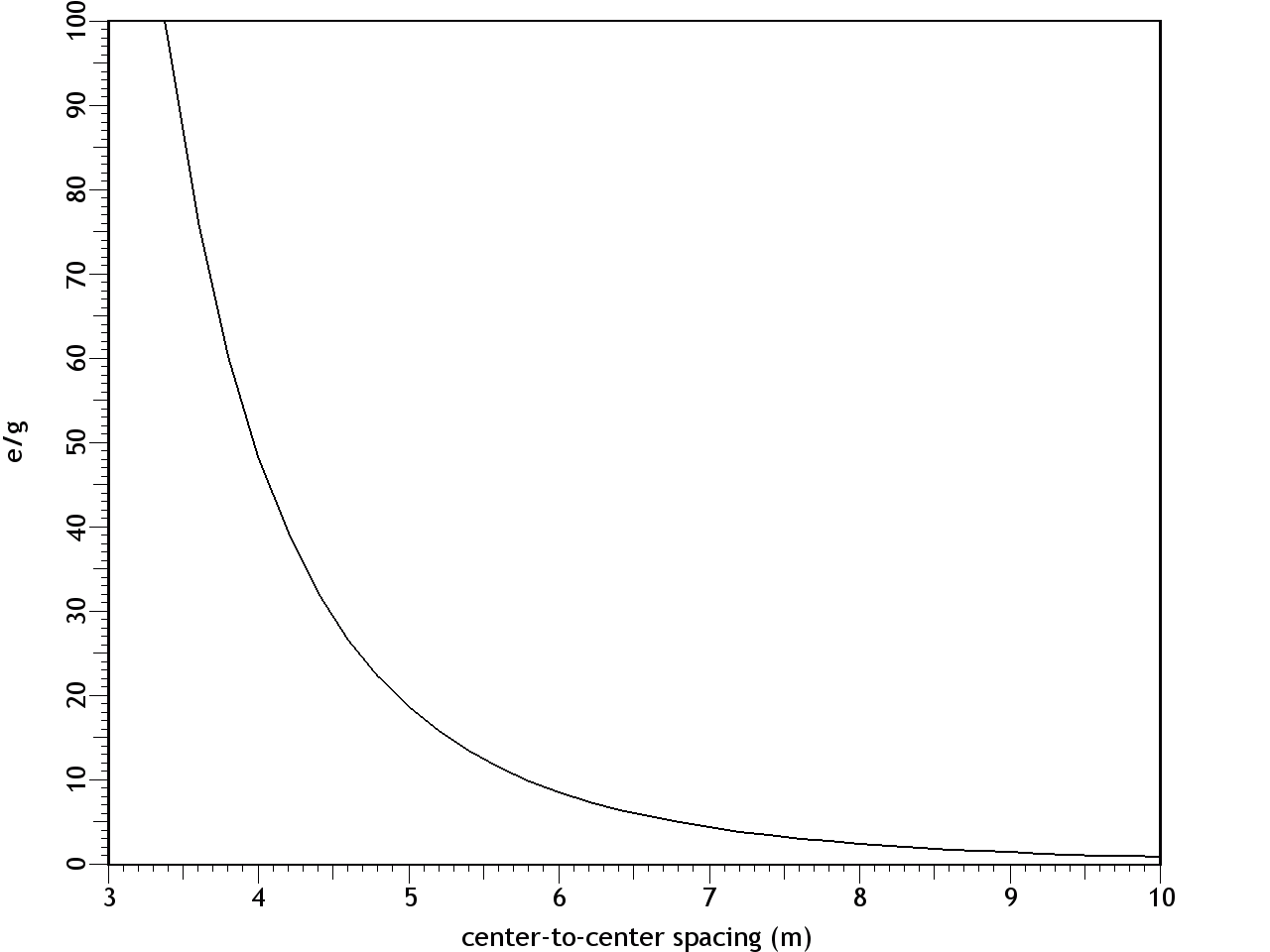
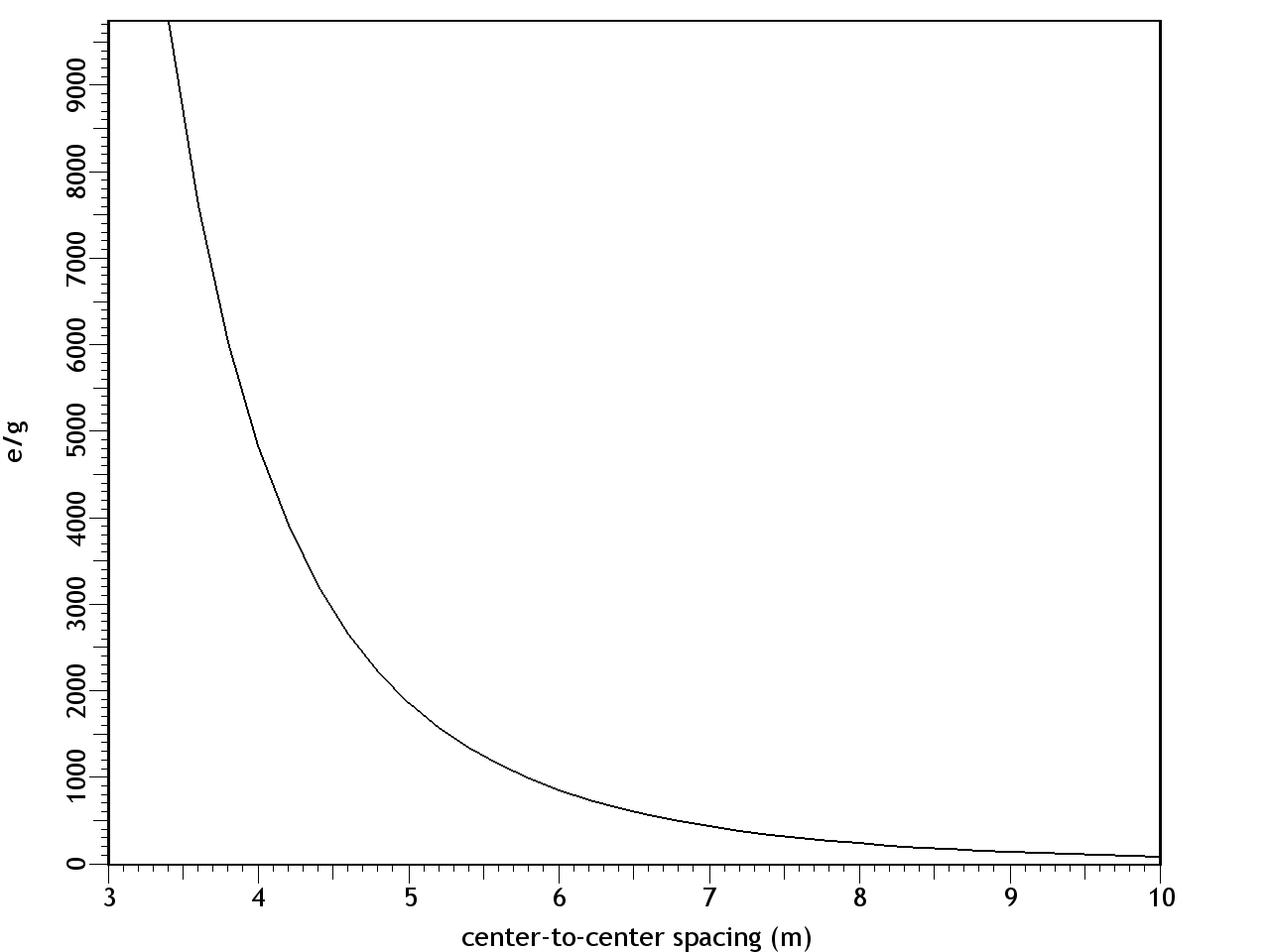
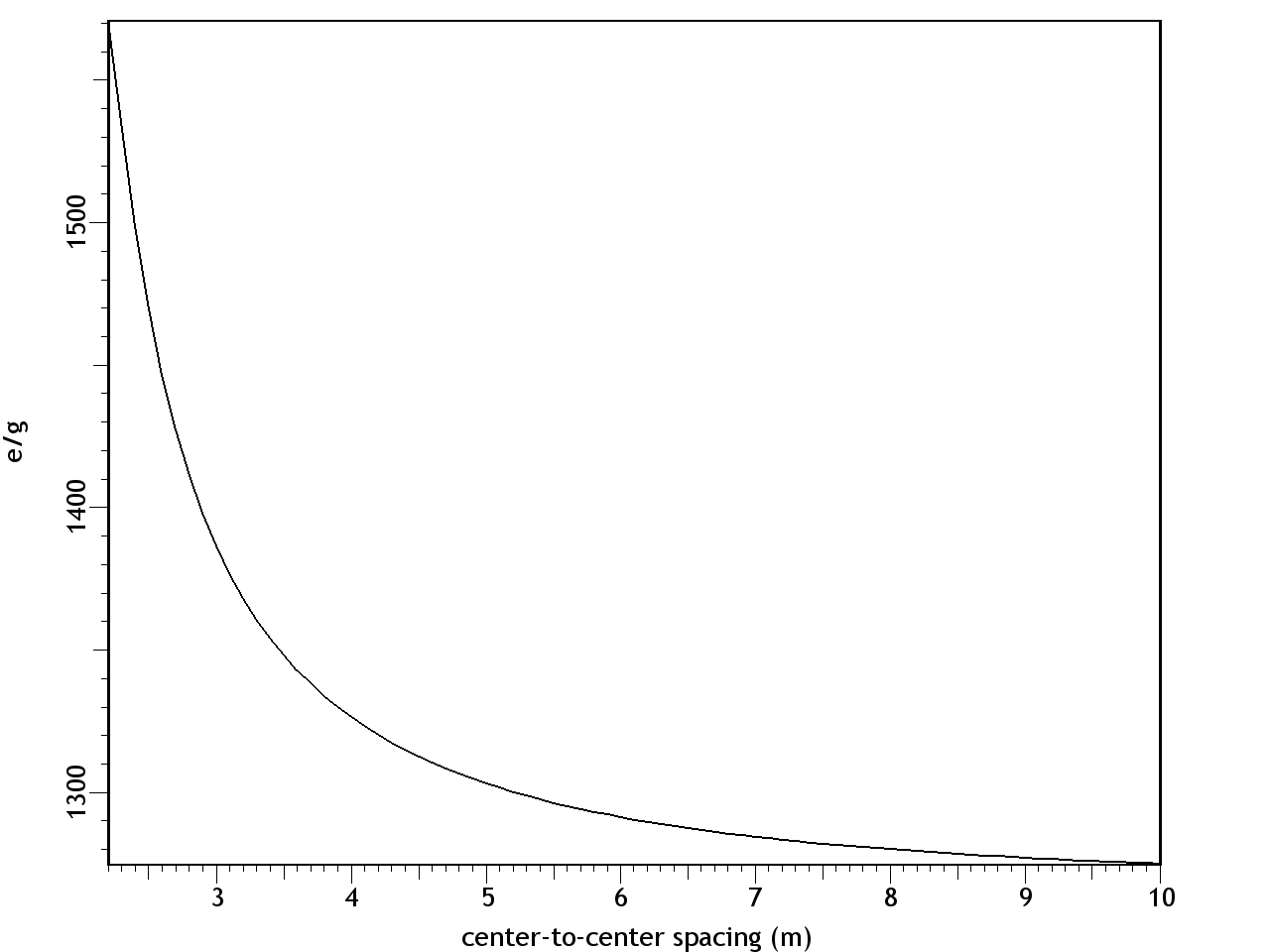
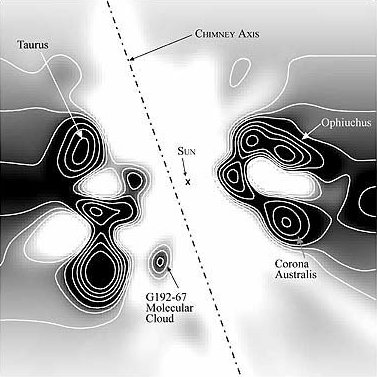
Equation 2. Electricity F = Eq1q2/d2 where: F = force (newtons) E = electric constant q1 = first charge (coulombs) q2 = second charge (coulombs) d = distance between centers (meters)

 

 

The results are shown in Figure 9. At a separation of 9.6 m, the e/g ratio was 1, so the electrostatic repulsion was equal to the gravitational attraction. With decreasing distance, both the gravity and the electric field increased by the inverse square law, while the effects of the electric force increased far more rapidly, because it's the stronger of the two forces.

 

 

Figure 9. Ratio of electric and gravitational forces between Debye cells, per the center-to-center spacing, with 1 charged particle in 10¹⁵ neutrals. In this graph, e/g greater than 1 is net repulsion.

 

 

At higher degrees of ionization, the electric force was even more overpowering. Figure 10 shows the forces with 1 charged particle in 10¹⁴ neutrals — still a modest charge for a dusty plasma.^9:74 At a spacing of 10 m, the electrostatic repulsion was already 82 times more powerful than gravity.

 

 

Figure 10. Ratio of electric and gravitational forces between Debye cells, at 1 charged particle in 10¹⁴ neutrals. In this graph, e/g greater than 1 is net repulsion.

 

 

The inescapable conclusion is that in this electrostatic configuration, there is no chance of gravity forcing the collapse of the matter, since there is a far stronger force opposing it. And note that this isn't even taking hydrostatics into account, which would provide yet another opposing force, if the Debye cells were to come into contact with each other. Thus it's easy to understand why dusty plasmas ordinarily do not collapse under their own weight, begging the question of how they ever could.

 

In search of the answer to that, we can make a more careful examination of the trigger. First we can consider supernovae. These release large quantities of UV radiation, which photo-ionize matter in the vicinity.^9:79 But increasing the degree of ionization will increase the electrostatic repulsion, so that's no help.

 

The other effect of a supernova is the release of particulate ejecta, and this is what supernovae have in common with gas cloud collisions as the triggers for dusty plasma collapses — they both involve the collision of two clumps of particles, which would have already resolved into so many Debye cells. So the collapse has something to do with Debye cell collisions.

 

Figure 11. Debye sheaths stretched into comas by ram pressure stripping.

The effect of such collisions is simple: the drag force on the sheaths will be greater than on the nuclei, resulting in the Debye sheaths becoming like cometary tails, trailing away from their parent dust grains, in the direction of the drag force. (See Figure 11.)

 

The significance is that the net electric force goes from slightly repulsive to strongly attractive. The dominant force acting on the sheaths will no longer be repulsion from other sheaths, since there is now a nearer nucleus. Likewise, the nuclei are attracted to sheaths that are now floating in the intercellular space.

 

The actual electric field would be impossible to calculate without knowing exactly how much drag force was applied to the sheaths, such that the geometry of the comas could be estimated. But just to establish a baseline, the forces were calculated with the sheaths maintaining their general form, yet shifted to the center of the intercellular space, as in Figure 12. This will underestimate the electric force, because of the greater distance between charged particles, and because of the inverse square law. It is also unrealistic, since there will be nothing to keep the sheaths from dispersing. Still, this will be mathematically useful, to establish the bare minimum electric force.

 

 

Figure 12. The left pane depicts resting Debye cells. The right pane depicts Debye sheaths that have been stripped off the nuclei by friction in a collision.

 

 

The results are shown in Figure 13, with both e & g now being attractive. At a center-to-center spacing of 10 m, the electric force is already 3 orders of magnitude stronger than gravity.

 

 

Figure 13. Ratio of electric to gravitational forces, per the center-to-center spacing, with 1 charged particle in 10¹⁵ neutrals, and with the Debye sheaths stripped off of the dust particles. In this graph, e & g are both attractive.

 

 

This has several implications.

 

First, the dusty plasma will definitely implode, and the implosion will be much more vigorous than a gravitational collapse.

 

Second, the e/g curve is very different from the Jeans Instability. With only Newtonian forces taken into account, the gravitational collapse can only proceed at the rate allowed by radiative heat loss, which is extremely slow. But the electrostatic attraction increases dramatically during the collapse. This provides the additional force necessary to overshoot the hydrostatic equilibrium and continue to compress the matter into a star.

 

Figure 14. Local Chimney

© 2003 UC Berkeley

Third, Feynman's "like-likes-like" principle is actually operative both at the scale of Debye cells, and at the atomic scale. Supernovae are better triggers for star formation than gas cloud collisions, and now we can understand why. Initially, a nearby molecular cloud gets photo-ionized from the UV radiation from the supernova. This helps atoms form into molecules, and molecules into dust grains, which wouldn't have happened without the liberation of electrons, to relieve the shell repulsion. With dust grains comes the resulting Debye sheaths. These repel each other. But shortly thereafter, the particulate ejecta from the supernova arrive. The Debye sheaths are stripped from dust grains, establishing an electrostatic attraction between the cells. Now the Debye cells will collapse into a star. So it's a two-stage process, instantiating the same principle at two different scales, and supernovae just happen to provide the catalysts for both stages.

 

Finally, we should note that the body force from Debye comas is linear, and thus the dusty plasma will collapse moving parallel to the direction of the drag force. So dusty plasmas don't implode spherically — they first resolve into filaments, and then the filaments implode in a linear direction (as described in more detail in the section on Filaments). This is why the void left by the formation of the star in the middle of the Keyhole Nebula in Figure 1 is linear instead of spherical. Something similar might have happened when the Sun formed, with a linear filament collapsing, leaving a hot, low-density linear void known as the "local chimney." (See Figure 14.)

 

Calculations

Remote Discussions

Comments