Filaments

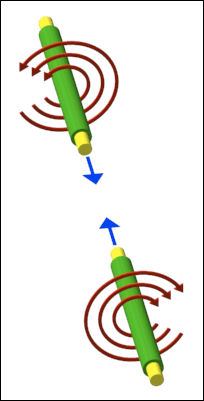
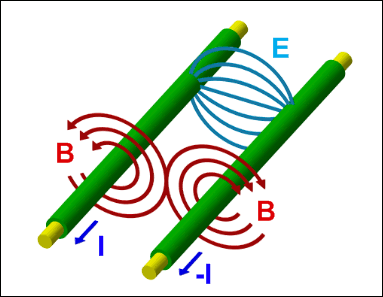
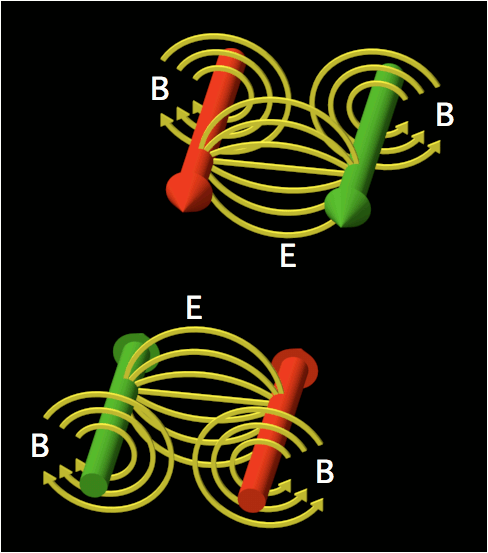
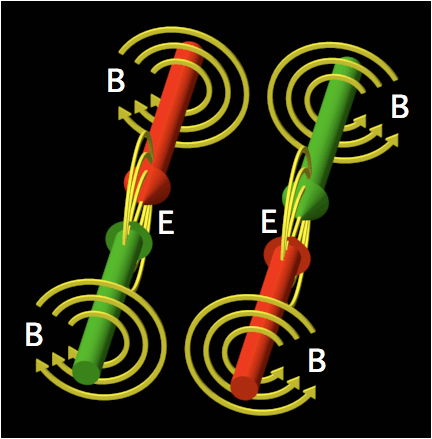
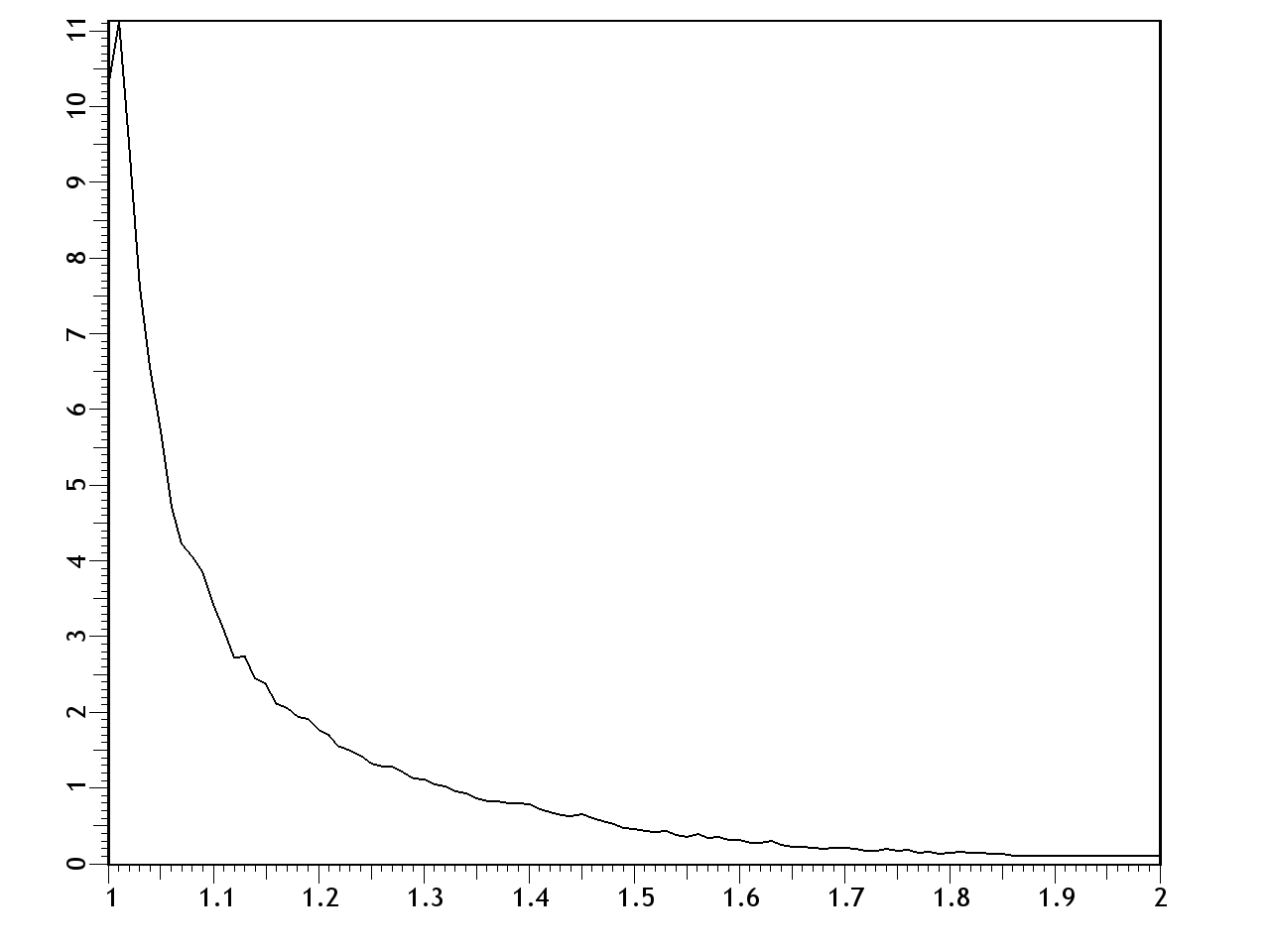
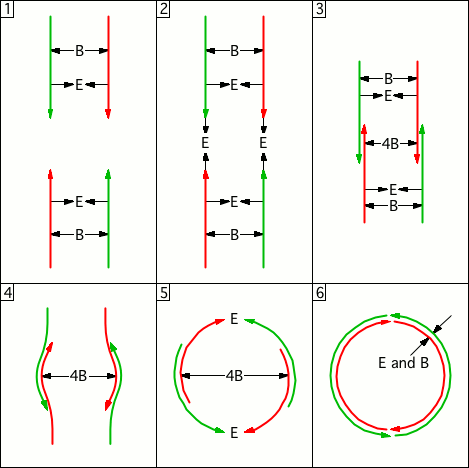
The section on Accretion identified a force far stronger than gravity that is responsible for the collapse of dusty plasmas into stars, planets, & moons. Now we can examine the dynamics of this process. Recent research has shown that giant molecular clouds first resolve into linear filaments, and then the filaments collapse into stars.¹^,²^,³ (See Figure 1.) The Universe is actually full of filaments of various sizes and shapes.⁴^,⁵ Both gravity and hydrostatic pressure object to this form, leaving only EM as the driving force. Some EM theorists have generalized the concept of Birkeland currents to explain the prevalence of filaments, but without establishing the electromotive forces at play, and without demonstrating that the currents would require material filaments. An electric current actually prefers a vacuum,⁶ and would evacuate the material in a filament by ohmic heating. So electric currents neither prefer filaments, nor cause them. Rather, the filaments are created by gas cloud collisions. The friction will be relaxed if they resolve into jets that tunnel through the opposing clouds. As they do, they'll stretch the Debye sheaths into comas, as in Figure 2, establishing a linear body force. So hydrodynamic jets produce electrostatic filaments. Once formed, they'll snap together. In other words, it's like grabbing a balloon that wasn't ready to "collapse" and stretching it into an ellipsoid with a high aspect ratio, creating a force that wasn't there in the resting condition. If we let go, the balloon will implode toward the center in a bidirectional linear motion, rather than a radial one.

Figure 1. Taurus Molecular Cloud.

Note that on a larger scale, the entire filament might not implode on just one point — the filament might break into segments that individually collapse into stellar systems, like beads on a string.⁷ There will be no guarantee that the stars will be perfectly spaced, or all of the same size, if there is no guarantee that the weak points in the filaments were evenly spaced.

On an extremely large scale, such as the stellar nursery in Figure 3, just the outsides of the tunneling jets are in contact with the surrounding matter, so that's where the Debye cell collisions are. And that's where the stars are forming. So where there is friction between the gas clouds, filaments are formed (not visible in Figure 3) that are parallel to the direction of the jets, which collapse into stars.

Pillars of Creation in the Eagle Nebula (M16).

The behaviors of the plasma at the center of the implosion are controlled by complex factors, and there can be a variety of outcomes. Naïvely, we might simply assume the conclusion and leave it at that — we have identified an inward force far more robust than gravity, and we have observed that this force is even stronger in the linear form (as opposed to radial) — then we know that one or more stars will form at the center of the implosion, so it doesn't look like there will be any surprises. But if we step through the whole process, and insist on a fully mechanistic description of each stage, we find that just the factors identified so far shouldn't produce a star — they will produce a violent collision of plasma at the center, but we have no reason to expect the plasma to stay consolidated. Rather, plasma collisions in the laboratory produce pancaked ejecta and/or counter-streaming tunnels that shoot through each other — they don't produce aggregates. So we're missing something.*¹⁶⁶²⁵

The next step is to consider the electrodynamic forces that will come into play. Insofar as the attractive body force is generated by ions, we have charged particles moving in a line toward the center. This constitutes a linear electric current of sorts. Thus it isn't that electric currents cause the filaments — it's that the filaments themselves are the currents. But note that the current isn't all going in the same direction — the two halves of the current are moving in opposite directions toward the center. And while moving charged particles generate magnetic fields, like charges moving in opposite directions generate fields that repel each other. (See Figure 4.) This has many implications, which need to be considered in turn.

First, let's derive the expectations if we can assume perfect symmetry in the line of plasma that is imploding. At the center, the plasma isn't actually going to collide violently — the opposing magnetic fields will brake the plasma. And note that the strength of the magnetic fields is proportional to the velocity. This has its own significance. Imagine shoving two bar magnets together, with their like poles facing each other. Without the magnetic fields, the two bars would collide. With the magnetic fields, the bars might never actually come into contact with each other — the magnetic force might get the bars to bounce off each other without even touching. But what if the magnetic force relaxes as the two bars are decelerated? They won't collide violently, but they won't bounce off of each other due to magnetic repulsion either — rather, they will collide gently. Now imagine that these are two plasma streams colliding — they won't pancake, or tunnel through each other — they'll just get to the center and stop, where other forces will take over, accomplishing the final consolidation of matter into one big star.

Figure 5. Opposite charges (I) traveling in the same direction generate opposing magnetic fields (B). At relativistic speeds, these approach the strength of the electric field (E) that attracts the opposite charges. And B doesn't fall off with the square of the distance like E, meaning that B has more influence once the charges are separated, and will organize them into two parallel charge streams.

On closer scrutiny, the formation of one big star at the implosion point isn't the only possibility. Each half of the filament is net neutral, meaning that both positive and negative charges are present. And just as like charges traveling in opposite directions generate magnetic fields that oppose each other, the same is true of opposite charges traveling in the same direction. (See Figure 5.) A subsequent section (i.e., Energy Budget) establishes that the collisional velocity could be as high as 0.86 c. Approaching the speed of light, the magnetic force becomes as powerful as the electric force. The significance is that we can expect to see charge separation within the imploding streams, due to the magnetic force.⁸ Thus it isn't going to be a filament imploding as two opposing streams of quasi-neutral plasma — the streams will be split into positive and negative strands.

So in total, there will be four different charge streams — two positive and two negative, with one pair coming in from one direction, and with the other pair coming in from the other. (See Figure 6.) The implication is that the two positive streams will repel each other, for both magnetic and electric reasons, and likewise for the negative streams, but oppositely charged streams will not have any magnetic repulsion between them, and the electric force will be attractive. (See Figure 7.) Hence the positive stream coming in from one direction will split off and collide with the negative stream coming in from the other direction. The two collisions will be braked partly by nearby opposing magnetic fields (just not as much as they would have been in a head-on collision) and by particle collisions when the opposing streams fuse. The result will be two stars, of roughly the same size.

This is a non-trivial property of the present model. Roughly 1/3 of all stars have binary companions,^9:155 most of which are very near in size. (See Figure 8.) This is typically attributed to fragmentation of the giant molecular cloud from which the stars condensed.^10:355 But no plausible mechanism has been proposed to account for such an even split. And for the binaries to end up in close proximity to each other, both halves must implode toward each other, forming stars right at the boundary, which is a theoretical problem that isn't even directly addressed. The present model explicitly allows the formation of one large star, if all of the matter in the filament implodes on the same point, or two small stars of roughly the same size, if the filament is separated into positive & negative strands that collide with their opposites coming from the other direction. This leaves any other combination as the rare exception, which is consistent with the statistics. Our Sun might be an example of the former case (i.e., one large star instead of two small ones), having no binary companion, and being 2~3 times larger than most binaries.

Figure 8. Comparison of the magnitudes in binary systems (per the Washington Double Star Catalog),¹¹ showing that most binaries are within 10% of the magnitude of their companions.

Once the two halves of the filament collapse into two stars, there will be no guarantee that they will remain in proximity to each other, forming a binary system. If the implosion loses little energy to magnetic braking, the newly formed stars will move away from each other far too quickly for mutual gravitational capture. If so, the result will be two singletons careening through the interstellar medium, instead of one binary system at the center of the original dusty plasma. Thus it's possible that more stars form as binaries, but only 1/3 of them stay associated.

Figure 9. Toroidal plasmoid formation. The arrows for the positive & negative charge streams (green & red) show the direction of the particle motion, while the arrows for the B & E fields are outward for repulsion and inward for attraction.

Two charged-separated halves of the filament approach each other (as depicted earlier, in Figure 6). Opposite charges are steered toward head-on collisions, for both electric and magnetic reasons.
Nearing the collision, an E-field develops between opposite charge streams, pulling them together (as depicted earlier, in Figure 7).
As the streams burrow through each other, the electric force is satisfied locally, so there is no longer any attraction between the strands in that segment. But the B-field between the strands gets quadrupled, because two repulsions have been doubled.
The lack of an attractive E-field, and the quadrupled repulsion from the B-fields, force the strands to bulge outward. The effect is the greatest where these factors have been present the longest (i.e., where the collision first started).
If the charge streams successfully burrow all of the way through each other, and continue out the other side, due simply to their pre-existing momenta, an E-field between the opposite charges gets re-established, steering the streams toward each other. The B-fields generated by the opposing streams (not shown) also favor a head-on collision, as they did in the first panel. (See Figure 10 for how the opposite charges in one strand become coaxial.)
The four individual charge streams finally resolve into a continuous loop. There will be a toroidal magnetic field wrapping around the annular axis that will keep the streams organized. Electrostatic repulsion between like charges will distribute them evenly around the loop, while attraction between opposite charges will keep the opposing streams bound together.

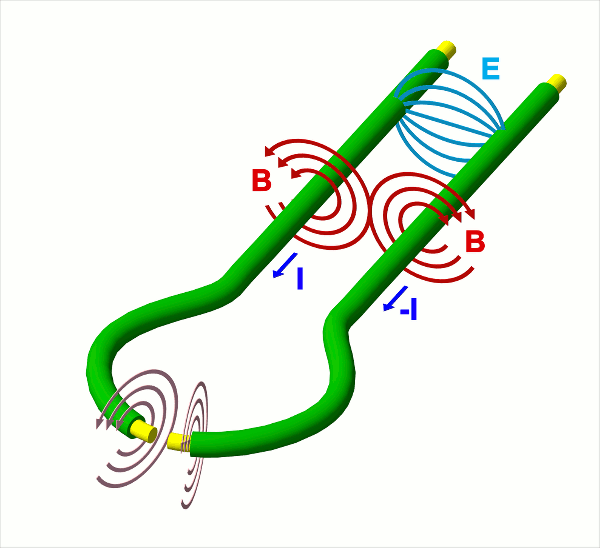
Figure 10. Opposite charges (I) traveling in the same direction generate opposing magnetic fields (B), but if the two charge streams are redirected to collide head-on, such that opposite charges travel in opposite directions, the magnetic fields reinforce each other.

Electrical resistance between the counter-streaming positive & negative charges will reduce the relative velocity between them. As this happens, the toroidal magnetic field will relax, eventually to the point that the toroid will fall apart. But starting with extreme angular speeds, the plasma will be a near-perfect conductor. So it will take a long time for electrical resistance to slow down the plasma.

In a much shorter period of time, the toroid would fall apart due to the centrifugal force from the extreme angular momentum. There will also be an outward force from the compression of the toroidal magnetic field on the inside of the loop. Both of these factors would tend to increase the radius of the toroid. There will be no centripetal force per se, but there will be a tensile force running through the charge streams that will prevent the radius from being increased. The section on Accretion established that in charge-separated matter such as plasma, there is an electric body force pulling inward. If the plasma is in annular form, this would be more properly called an annular tensile force. With this trying to decrease the radius, and with the centrifugal and magnetic forces attempting to increase it, the radius will stabilize when all of the forces come into equilibrium. Possible evidence of such a toroidal plasmoid is cited in the section on Supernovae, and the star in question (i.e., Mira) appears to have a major radius equal to the orbit of Pluto around the Sun. If Mira has the same volume as the Sun, though in toroidal form instead of spherical, the minor radius would be 3486 km (i.e., roughly equal to the radius of Mars).

Roughly 90% of the stars in the Universe are in the main sequence, and are probably spherical, like our Sun, while 10% of the stars have a fundamentally different property set. These stars include quasars, blazars, magnetars, pulsars, white dwarfs, and the central stars of planetary nebulae. Subsequent sections demonstrate that many of the properties of such stars are difficult or impossible to explain if the star is a sphere, but easy to explain if it's a toroidal plasmoid. So the present thesis is that all stars are formed by imploding filaments, with 90% of them getting compressed into spheres, and with 10% of them falling into the toroidal form as described in Figure 9.

← PREV	Powered by Quick Disclosure Lite © 2010~2022 SCS-INC.US	NEXT →