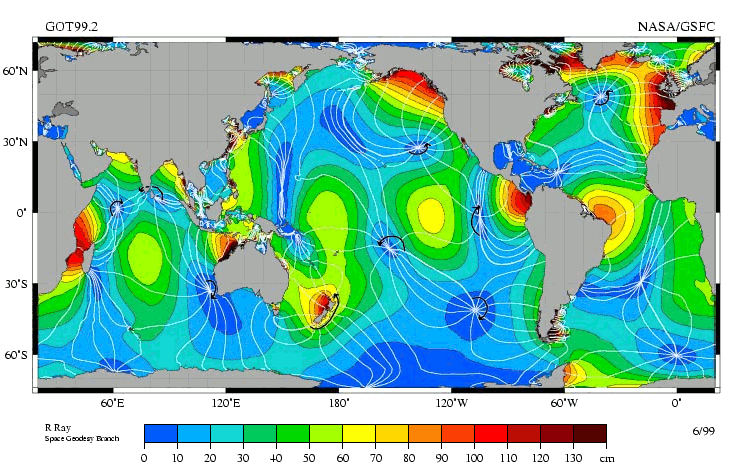
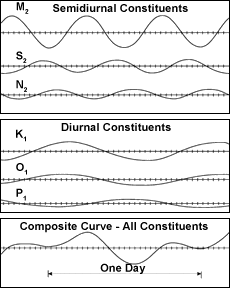
© Charles Chandler

 

For a planet with a crust that has been solid for at least a couple million years (if not longer than that), the Earth is surprisingly dynamic. Earthquakes, volcanoes, and tectonic plate motion are driven by one or more unknown energy sources. A full accounting of the forces that keep churning inside the Earth remains outside our reach, but everyone is in agreement that tidal deformation is one of them, and both earthquakes and volcanoes are more likely when tidal forces are at their maximum. Yet there are some big gaps in our understanding of tides.

 

Figure 1. Crustal deformation due to tidal forces. Red = up, blue = down, with the Moon directly over 30° North.

It has been known since ancient times that the oceanic tides are directly related to the position of the Moon, and to a lesser extent, the Sun. We now know that it isn't just the oceans that are affected — the crust also flexes, as much as 1.11 m at its peak. The period isn't close to any of the crust's harmonic frequencies, so resonance isn't a factor, and the crust simply responds directly to the force acting on it at the time, with roughly a 2 hour delay to the maximum effect, due to the momentum built up during the forcing. (See Figure 1.) The oceans, on the other hand, have standing waves (λ ~6700 km), producing extreme tides where the coasts fall midway between the null points, and where the angle of the coastline is roughly perpendicular to the waves, thereby conserving all of the constructive interference. (See Figure 2.) Such factors make oceanic tides a lot more complicated. The present article doesn't delve into such complexities, and rather addresses just the primary forcing mechanism(s), as evidenced in crustal tides.

 

 

Figure 2. Oceanic tides from lunar forcing, credit R. Ray. Colors indicates amplitude, with white cotidal lines at 1-hour intervals. The curved arrows around the null points show the direction of the advancing waves.

© 2000 NASA

 

 

Crustal tides start out easy enough to understand. They are responses to lunar and solar gravity, and because the Moon is nearer, it has a greater effect. The Sun's gravity is actually 179 times greater than the Moon's. The Sun might be further away, but it is much, much more massive. (The image at left shows the distance between the Earth and Moon relative to their sizes. At that scale, the Sun would be half a meter across, and about 50 meters off-screen.) So at first blush, we might think that the tidal cycle should obey the position of the Sun first, and the Moon second (if at all). But there is a hidden significance to the proximity of the Moon. Gravity obeys the inverse square law, meaning that its force falls off with the square of the distance, asymptotically approaching zero infinitely far away. Since the Sun is much further from the Earth, its inverse square curve has already flattened out. As a consequence, the gravitational tug from the Sun is pretty much the same, from the near side to the far side. And if everything (near and far) is getting tugged the same amount, there won't be a bulge on the near side. But the Moon is much closer, and because of this, its inverse square curve still has some curve to it, meaning that the Moon's gravity is stronger on the near side than on the far side. Thus the effective tidal force from the Moon (1.13 × 10⁻⁶ N/kg) is 2.23 times greater than from the Sun (5.05 × 10⁻⁷ N/kg).¹

 

So what enables the crust to flex? That would be the elasticity of the rock. Even though solids are considered to be incompressible, they still have a little bit of throw. For granite, the modulus of elasticity is 50 GPa, meaning that for every pascal of pressure (+/−), the rock will compress/expand by 50 billionths of its total length. (Possible differences in the compressibility under the elastic and plastic regimes are outside the scope of this article.) So if we take a column of granite that is 6371 km tall (i.e., the radius of the Earth), with a cross-section of 1 m², and apply the combined lunisolar tidal force to it (i.e., 1.63 × 10⁻⁶ N/kg), how much will the rock flex?

 

First we cut the lunisolar force in half, because it goes from its maximum at the surface of the Earth down to nothing at the center. (The tidal bulge is created by the difference between gravity at the surface and at the center.) So the average force acting on the entire column is 1.63 × 10⁻⁶ / 2 = 8.17 × 10⁻⁷ N/kg.

 

Now we find the mass of the column. Granite has a density of 2650 kg/m³, and our rock column has 6,371,000 m³ of it, for a total of 1.69 × 10¹⁰ kg.

 

To find the total force, we just multiply the mass times the acceleration, which comes out to 1.38 × 10⁴ N. Despite the fact that gravity is a body force, we're going to treat it like pressure being applied just to the top surface of the column (1 m²), and for our purposes, it doesn't matter where the force came from. So we'll use 1.38 × 10⁴ N/m² as the force applied to the top.

 

Then we divide the force by the modulus of elasticity to find the compression ratio. So that's 1.38 × 10⁴ N/m² / 5.00 × 10¹⁰ GPa = 2.76 × 10⁻⁷.

 

Now all we have to do is multiply the compression ratio by the total height of the column, to find the total throw under that much force. 2.76 × 10⁻⁷ × 6,371,000 m = 1.76 m. Curiously, the total crustal deformation on the near side is actually only 1.11 m. (See Primary Tidal Constituents.) So we're missing 0.65 m of the throw that should be there, given the gravitational loading, and the modulus of elasticity.

 

Figure 3. Tidal bulges.

Figure 4. The primary constituents of tidal forcing, courtesy US Navy.

And then there is another curiosity that has to be investigated — there is an unexplained tidal bulge on the far side of the Earth, which achieves a maximum height of 0.69 m. (See Figure 3 and Figure 4.) This is tough to reconcile with Newtonian principles. (See Helmer Aslaksen's page for an overview of the attempted explanations.) We can draw pictures of it, and talk about it with Newtonian jargon. But the bare-faced fact is that it shouldn't be there. For example, something that causes a bulge on one side relieves pressure at the center, allowing the sides to collapse inward. If the crust is rigid, it will transfer force, creating a bulge on the far side. But the crust experiences no lateral elastic stress undergoing such a small deflection over such a long distance, so there is no effective rigidity to transfer the force.

 

If there is no Newtonian explanation for the opposing bulge, this can only mean that it is caused by non-Newtonian forces. The only other fundamental force present on a global scale is electromagnetism, and interestingly, EM is capable of producing a far side bulge.

 

The previous section established that the geomagnetic field would only be possible if the Earth was comprised of charged double-layers, caused by electron degeneracy pressure (EDP).²

Under extreme pressure, atoms are forced so close together that the outer electron shells fail, and the electrons are expelled, leaving +ions behind. The expelled electrons congregate at a higher altitude, where there is less pressure, and thus there is room between the atoms for extra electrons. So the core is positively charged, while the surface is negatively charged. Since the prime mover is gravity, which is [relatively] constant, the charge separation is stable, creating current-free double-layers (CFDLs). In other words, there is a charge separation, but even in the absence of sufficient insulation, the charges don't recombine, because the forcing mechanism is still present. Hence the double-layers are [relatively] current-free.

Now we should amend that, because with tidal forcing, the gravity isn't perfectly constant. Rather, the Earth's gravitational field is being modulated by fields from the Sun & Moon, causing fluctuations in the pressure. The implication for CFDLs is that inside the Earth, one of those isobars represents the depth at which EDP begins, and if the isobar moves, the charge separation moves with it. Below that isobar are +ions, and above it are −ions. If the pressure relaxes (because it is relieved by the Moon's gravity), the EDP isobar shifts downward. When it does, rock that had been forcibly ionized can now engage in electron uptake. And when the pressure is restored, those electrons are expelled again. This flow of electrons constitutes an electric current. Since the crustal tides have two ebbs and two flows per day, that's four surges of current per day. And note that the tidal range is roughly the same from one day to the next, so whatever got ionized during the ebb is the same stuff that gets de-ionized during the next flow, and this repeats, over and over. Since the tidal forcing is only 1.67 × 10⁻⁷ that of the Earth's gravity, the isobar in question only shifts an estimated 1.06 m. But day after day, it's the same 1.06 m that is getting alternately ionized and de-ionized, four times a day. Ohmic heating from these currents will accumulate, making this a very hot layer. By a variety of lines of reasoning, the depth of this EDP isobar is identified as the Moho, which averages 35 km below the surface, and which is examined in greater detail in the next section. For now, all that is important is that there is a layer that is heated by electric currents at the threshold for EDP.

 

By the principles of EDP, electrons expelled by the greater pressure at depth will be forced upward. If the pressure is relaxed, we'd then expect those same electrons to simply flow back down again. But the rock in the solid crust above the Moho isn't such a great electrical conductor, so this will take a lot of work. At the same time, once the Moho gets heated, electrons can flow more easily through it than through the surrounding rock, because hotter rock (especially if it gets molten) is a better conductor. Thus the more likely source of electrons will be a remote region that is currently expelling them, with the electrons flowing through the Moho to satisfy the demand. In other words, while tidal gravity is lifting one area, creating a demand for electrons, 90° away on the sphere is at low tide, and electrons are getting expelled by increasing pressure. If the Moho is a good conductor, the most economical way to relieve the electrical stresses created by both high and low tides is for the electrons to flow from the low to the high region. Thus the Moho is not only heated by local currents — it serves as a conduit for remote currents. The implication at the far side of the Earth is that the demand for electrons on the near side creates a deficiency of them on the far side. This leaves a positively charge crust sitting on top of a positively charged mantle, and electrostatic repulsion between the two pushes the crust upward, creating the far side bulge.

 

Telluric currents associated with tides are well-known. Such currents are typically attributed just to the flow of water in the oceans, and no explicit study of inland tidal ionization has been located thus far. But an indirect measure might have been found by a study of lightning in North Dakota, USA (which is definitely inland). In 10 years of data, the cloud-to-ground strike rate averaged 22% greater at high tide, which was statistically more significant than the other factors normally associated with lightning induction, such as topography, vegetation, and infrastructure.³ Since 85% of all CG strikes are from a negative charge in the cloud to a positive charge in the ground, this suggests that the ground had a stronger positive charge at high tide. And indeed, if the surface is elevated by tidal forcing, the pressure underneath is relaxed, enabling electron uptake at depth, reducing the net negative charge at the surface.

 

The correlation between tidal forcing and atmospheric electrification can also be seen in the yearly fluctuations of the Earth's fair weather field. When the Earth is closest to the Sun, the tides are stronger, and so is the electric field. (See Figure 5.)

 

 

Figure 5. The fluctuation in the Earth's electric field peaks at perihelion (red bars), and hits its minimum at aphelion (green bars), courtesy Constantine Thanassoulas.

 

 

So how much electrostatic repulsion would it take to hoist the crust 0.69 m on the far side? We know that the lunisolar gravity (i.e., 1.38 × 10⁴ N/m²) is capable of hoisting the crust 1.76 m. And we're looking for the force necessary to hoist the crust 0.69 m. So we merely have to find the ratio of the deformation distances, and multiply the gravitational force by that amount, to find the electric force. This comes out to 5.39 × 10³ N/m². Considering that the Moho is 1.06 m thick, we can calculate the charges necessary to generate the Coulomb forces at that distance. The result is 5.13 × 10¹⁵ electrons per square meter of the Earth's surface, or 5.13 × 10¹⁵ electrons per cubic meter of Moho. Considering that there are 1.58 × 10³⁰ atoms in a cubic meter of granite, that's the equivalent of 1 ion per 3.09 × 10¹⁴ neutral atoms, which is not an unreasonable degree of bulk ionization.

 

And with this we can account for the discrepancy that we found earlier, between the amount of tidal deformation that gravity should accomplish on the near side (1.76 m) versus how much it actually accomplishes (1.11 m), leaving a difference of 0.65 m. We're seeing a far side bulge of 0.69 m. So that's where the force went. In other words, given the gravitational forces acting on the near side, it would have popped up 1.76 m. But as it starts to rise, it creates a deficiency of electrons. Being connected to the rest of the globe by the conductivity of the Moho, the far side can more easily supply the electrons. This generates a force on the far side that hoists the crust there. How much? The same amount that the near side throw is attenuated. So both bulges are coupled by the electrical conductivity of the Moho.

 

Of the total forcing (1.76 m), why does 63% of it show up on the near side, and only 37% of it on the far side — why don't both sides get elevated the same amount? This would be evidence of resistance. The Moho, as a supercritical fluid, might be an excellent conductor — so much so that force can be transferred to the far side of the Earth. But nothing is a perfect conductor, and resistance is always a factor. In this case, resistance impedes the transfer of force to the far side. As an analogy, consider two sealed jars, both half full of water and of air, and with the jars connected by a garden hose 10 m long. All other factors being the same, the air pressure inside both jars will be the same, if the water can flow freely through the garden hose. Now if we apply a vacuum pump to one of the jars, to evacuate some of the air, we'll reduce the air pressure inside that jar, and we'll expect the water level to rise inside that jar, until the pressure has re-equalized between the two jars. This requires that the water level inside the other jar go down the same amount. This will eventually happen, but on the short term, the equalization will be limited by friction inside the water hose. Now if we give the water a high modulus of elasticity, we might see the water level rise toward the vacuum inside the one jar, more than it is falling inside the other jar, because not all of the force got transferred through the water hose instantaneously. Of course, this analogy has the water going up in one place, and down in the other, as the equal-but-opposite reaction, while with electrostatic forcing, the crust rises on both the near and far side. But in both cases, the coupling isn't direct if there is resistance to the equalizing flow.

 

Before we're done, we have to acknowledge some of the complexities that have been overlooked. We have two different forcing mechanisms, and several types of expansion. On the near side, we have gravity lifting the rock, so we got the expected expansion from the modulus of elasticity for granite, even though we didn't differentiate between the elastic regime above the Moho, and the plastic regime below it. We should also note that there is reason to believe that the Moho is hot enough to have undergone the transition to a supercritical fluid, which is compressible, like a gas. Then, on the far side, electrostatic repulsion is pushing up on the crust. It would be more accurate to say that the Coulomb force causes the matter to expand, by weakening covalent bonds, and creating more space between atoms. These effects are not just felt on the underside of the crust — they're felt throughout the crust, and beyond. The study cited above noted the increase in CG lightning at high tide. In addition to fluctuations in the surface potentials, there are also fluctuations in charge density in the atmosphere, all of the way out to the ionosphere.^4,5 So the Coulomb force originating in the Moho can drive crustal expansion far from the source. While the effects of pressure within the elastic regime are fairly well-known, compressibility within the plastic regime has received less attention, and the effects of powerful net charges on rocks at extreme pressures haven't been explicitly studied. So it will be up to future research to fill in the details.

 

Still, it would seem to be a worthwhile study, since EDP is starting to look like a general principle with wide applicability. For example, previous sections demonstrated that the Sun is comprised of charged double-layers. And while the Sun's gravity disrupts the Earth's interior, the Earth's gravity does the same thing to the Sun — when external gravitational forces are at their peak, there is an increase in the number of sunspots, and thus the number of CMEs.^6,7,8,9,10

 

 

Figure 6. Correlation between the Sun's movement and sunspot cycles, courtesy Paul D. Jose. The pattern continues to match up to the present (2012). The 5 curves, from top to bottom are:

1) the distance from center of solar system mass to center of Sun,
2) the radius of curvature of Sun's path,
3) the rate of change in the angular momentum about the center of mass,
4) the rate of change in the angular momentum about the center of curvature, and
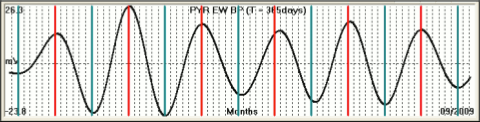
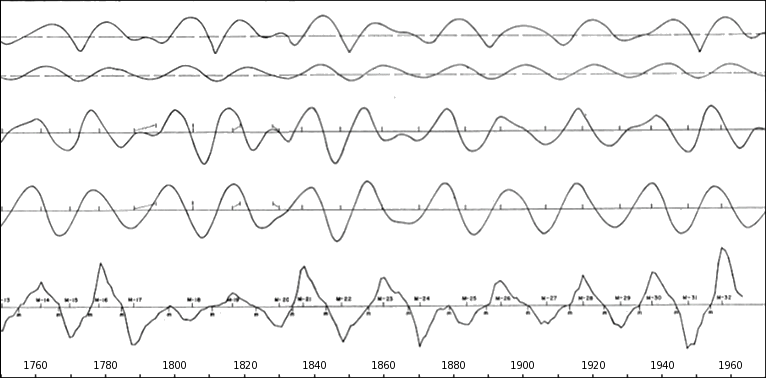
5) number of sunspots (up is one magnetic polarity and down is the other)

 

 

Note that the forcing mechanism is on a 22-year cycle, while sunspots peak every 11 years. This suggests that some sort of internal oscillation causes the 11-year cycle, while every 22 years another set of forces comes into play, synchronizing the two cycles.¹¹ This stands up to reviews of long-term data.

 

The system becomes fully non-linear when we consider that proton storms from CMEs can modulate tidal forces here on Earth.¹² And those forces can, in turn, trigger volcanic eruptions and earthquakes.¹² But note that the present thesis suggests a different interpretation of the relationship. In a later section, volcanoes are described as electrical conduits, wherein the magma is kept molten by ohmic heating from a current flowing between the Moho and the surface. Accentuated crustal tides are thought to encourage the magma, by kneading the crust, but in the present model, the relationship is the other way around — the conductivity of the magma tube allows charge imbalances in the Moho to be satisfied locally, leaving less need to pull electrons from the far side, and thereby partially decoupling the antipodal tide. Thus the crust near the volcano flexes more freely. If this is correct, any accentuation in crustal tides near a volcano will be accompanied by a corresponding attenuation in the antipodal bulge, proving the coupling.

 

Calculations

Reference for Moho Thickness?