© Charles Chandler

 

Abstract

The forces responsible for earthquakes are explored. The expectations of existing models, such as mantle convection, are shown to be inconsistent with the observations. An alternative is to look at the electric and magnetic fields associated with earthquakes, though the origins of those fields are unknown, and the causal role that they might play has not been identified. The present work extends the hypothesis that the primary electric field is between the positively charged mantle below the Mohorovičić discontinuity, and the negatively charged crust above it. The charge separation is due to electron degeneracy pressure, wherein matter under sufficient hydrostatic pressure gets positively charged, and where the electrons that were forced out of the matter accumulate on its surface. As applied to layers within the Earth, the assertion is that matter below the Moho is under sufficient gravitational loading for forced positive ionization, and that the crust hosts the electrons expelled from the mantle. If the gravitational loading remained constant, the forced ionization would be static, and there wouldn't be any electric currents responding to the electric field between the mantle and the crust. But crustal deformation alters the pressure at depth. For example, if the crust buckles because of lateral pressure, the buckle relieves the gravitational loading on the underlying rock, since the lateral compression strength of the plate carries the weight, like a Roman arch. The reduction in gravitational loading allows electrons to flow back into the mantle that had been forcibly ionized. Interestingly, this flow of electrons generates ohmic heating, which causes the crust to expand. Since the crust has already buckled due to lateral pressure, further expansion increases the buckle, which is the prime mover. Thus there is a positive feedback loop, involving lateral pressure, which causes crustal buckling, which drives an electric current with its ohmic heating, which augments the lateral pressure. This runaway feedback loop is then responsible for the catastrophic failure of traction along the fault. This hypothesis compares favorably with the actual characteristics of earthquakes, including the sharp ramp-up of oscillations in the main event, the number, frequency, and magnitude of aftershocks, etc.

 

Earthquakes are caused by the relative motion of crustal plates. But the force that shifts the plates has not been identified. When the full extent of the mid-ocean ridges was realized in the 1950s, it was supposed that something was forcing magma to the surface, which then exerted pressure, pushing the plates apart, resulting in plate collisions elsewhere. But the ocean floors lack the pressure ridges that would certainly develop there, if anywhere, since the lateral pressure would be the greatest at the source of the pressure. Instead, the ocean floors are characterized by transform faults, indicative of sheared tensile strain. So the plates are actually being pulled apart. The mid-ocean ridges are just the consequence of magma that solidified on its way up, and then got pulled horizontally, not accomplishing a sharp 90° turn in the process.

 

 

Figure 1. The Mid-Atlantic Ridge and its transform faults.

 

 

The consensus now is that the plates are being pulled apart by crustal convection. The idea is that new crust forming at mid-ocean ridges is hot, and that it cools with age, making it more dense. At subduction zones, the heavier old crust sinks back into the mantle. Thus the plates are just the topmost aspect of a convective current. But this still isn't correct, as the following facts demonstrate.^1:45

In the plate tectonics context, heat loss should have its highest values in mid-ocean ridges, and it will be gradually reduced moving away from the central ridges, reaching its lowest values in trench and trench-arc gap regions, i.e., at depths of the Benioff zone, shallower than ~100 km. But the data² indicate that the mean heat flow value is about 60~80 mW/m² in oceanic or continental sites, independent of and despite idealized plate tectonics expectations. Also, heat flow values below 30 mW/m² are actually common in and near mid-ocean ridges, and values above 150 mW/m² are paradoxically common in trenches and back-arcs. The most characteristically contrary examples to standard expectations are those of Japan and Fiji-Tonga,³ where most of the deepest earthquakes actually occur, and alleged subduction of cold "lithospheric" oceanic slab is thought to occur.

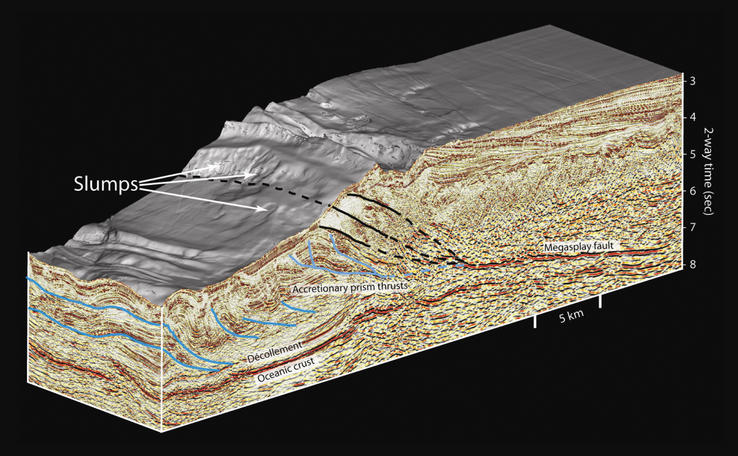
Table 1. Crustal powers, from Tassos & Ford (2005, pg. 46). Energy Type % tectonic friction 95.789 radiative heat loss 4.122 lava production 0.084 elastic wave energy 0.005 total seismic moment 100.000

With the coolest, heaviest rock rising in the mid-ocean ridges, and the hottest, most buoyant rock sinking back into the mantle, this is clearly not a convective system. And even if convection were sending the crust in the proper direction, the power isn't there — it takes a running average of 10¹⁵ watts to grind crustal plates past each other, which is 96% of the total near-surface power, while radiative heat loss is only 4%. (See Table 1.) If convection were driving plate motions, radiative heat loss would have to be equal to tectonic friction for the power budget to work.

 

So what provides the power to move the plates, if not convection?

 

Tidal forces are sometimes given credit for plate movement,⁴ by kneading the crust, resulting in slippage at fault zones. But inelastic and plastic deformation from tides only account for about 10¹² watts, which is 4 orders of magnitude less than the power consumed by tectonic friction.^1:46

 

Having exhausted the conventional power sources, without finding anything up to the task of overcoming traction in fault zones, we can only broaden the search to include other forces, such as the evidence of fluctuations in electric and magnetic fields associated with subduction, of which there is plenty.^5,6,7 Figure 2 shows a typical subduction fault.⁸ A description of the fault process follows.

 

 

Figure 2. Subduction in the Nankai trench off the Izu Peninsula, Japan, courtesy of the University of Texas Jackson School of Geosciences.

 

 

The rupture of a subduction fault starts with the slippage of the lithosphere with respect to the underlying asthenosphere, without loss of traction along the fault.⁹ This increases the lateral pressure at the fault. The pressure is felt throughout the plates, and all other factors being the same, the plates could buckle anywhere to absorb the stress. But as we see in Figure 2, the plates are thinnest where they have been ground down by previous plate movement, so buckling is more likely to occur near the fault. The lower (oceanic) plate has forces on both sides of it, but the upper (continental) plate has nothing above it, so it buckles upward. (This is what causes ground water levels to change in the days before a quake.¹⁰) When the fault ruptures, the buckle flattens back out again, with the leading edge of the continental plate advancing over the oceanic plate, like an inchworm moving forward as it straightens itself out.

 

Before and during the earthquake, there are distinctive signs of electromagnetism, including changes in electric fields, "earthquake lights" (which are corona discharges from tall, pointed objects),¹¹ and perturbations in the Earth's magnetic field.¹² All of these are typically attributed to the piezo effect,¹³ but that isn't correct. Certain types of crystals, including quartz, become electric dipoles under pressure. So mechanical forces can create electrostatic potentials. The converse is that such crystals can be made to do mechanical work when exposed to an electric field. (This is how piezo tweeters work.) But the dipolar field created under pressure doesn't extend much beyond the crystal itself. Furthermore, the quartz grains in the Earth are randomly oriented, meaning that the effects from individual crystals should cancel each other out, leaving no net piezo effect.^14:42 The likelier source of the electromotive force is electron degeneracy pressure, which can generate electric fields in all matter, regardless of the crystal lattice (or lack thereof, if the rock is molten).

 

Figure 3. Charge Separation Under Pressure At left is an abstract representation of a normal crystal lattice, using the familiar icon for an atom, and showing connections of electron shells. At right, extreme pressure has forced the expulsion of one of the electrons from the atom in the center. The expelled electron is to be found just outside, wherever there is room for it, while attracted to the positive ion by the electric force.

It is well-known that at high pressures, matter gets ionized.¹⁵ This is because of the Pauli Exclusion Principle, whereby no two identical fermions (i.e., particles with half-integer spins, such as electrons) may simultaneously occupy the same quantum state in the same location. If atoms are pressed too close together, the electron shells of neighboring atoms overlap, and the conflict forces the liberation of one of the electrons. The extra force required to do this accounts for the incompressibility of liquids and solids.^16,17,18 (See Figure 3.)

 

The same is true even for supercritical fluids — even though they're too hot for crystal lattices, and thus have a plasticity uncharacteristic of their subcritical solid regimes, once compressed down to the density of a solid, they become just as incompressible as subcritical solids.^19,20 This fact isn't salient in the larger body of studies that have been done on supercritical fluids at less extreme pressures, and there's actually one place in the phase diagram where supercritical fluids are compressible beyond even the ideal gas laws — just above the critical temperature. (See the Nelson-Obert charts, and the closely spaced density lines just above the CP in Figure 4.) Nevertheless, the fluid is as incompressible as ever once it achieves its solid density. (See Figure 5.) CO₂ at its critical temperature of 31 °C, when subjected to 300 GPa (i.e., 3 million bars), has a density of 1400 kg/m³, which isn't much above its solid density below the triple point. So supercritical fluids still have a modulus of elasticity beginning at the solid density, but that isn't what we'd call compressibility, certainly not in line with the ideal gas laws.

 

 

Figure 4. Carbon dioxide phase diagram. © 2000 FutureChem

Figure 5. Another representation of the density of the various states.21 In the solid regime, increasing pressure doesn't further compress the matter — it simply enables the closest packed arrangement even at increasing temperatures.

 

 

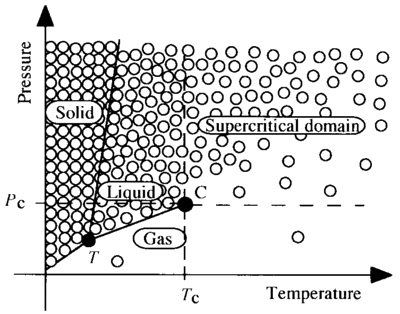
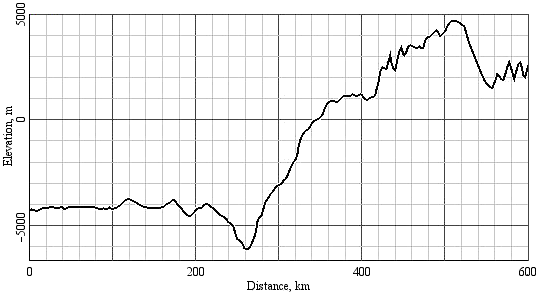
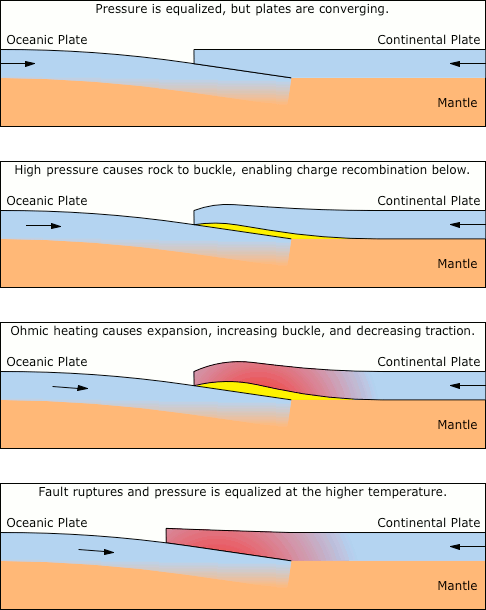
Electron Degeneracy Pressure $$P=\frac{h^2}{20m_em_p^{5/3}}\left(\frac{3}{\pi}\right)^{2/3}\left(\frac{\rho}{\mu_e}\right)^{5/3}$$ where: P = pressure h = Planck's constant me = mass of electron mp = mass of proton ρ = density μe = electron/proton ratio

Thus the Pauli Exclusion Principle holds even for supercritical fluids. Monoatomic matter above the critical point isn't constrained by covalent bonds. But when two atoms are forcibly pushed together, the first conflict will be between the outer electrons. If the pressure is greater than the ionization potential of the atoms, the conflict results in the expulsion of electrons, leaving a strong electrostatic repulsion between the positively charged atomic nuclei, and further compression has to fight the Coulomb force. This marks the transition from compressibility to elasticity, which is very different. The Quantum Mechanics term for this effect is electron degeneracy pressure (EDP), though the Pauli Exclusion Principle predated QM, and is not reliant on it.

 

If the pressure is coming from gravitational loading, it increases with depth, meaning greater compression, and atoms packed closer together. At the threshold for EDP, electrons are expelled, and they have nowhere to go but up, where they will find room between atoms that aren't as tightly packed. Thus the expelled electrons are forced to a higher altitude, leaving positive ions below.

 

The implication not typically considered is that a charge separation has occurred, creating current-free double-layers (CFDLs) — they are layers of opposite charges, with a powerful electric field between them, but there is no current responding to the field, because something prevents it. Usually a sustained charge separation requires an insulator, but in this case, EDP separates the charges and keeps them separate. And gravity is forcing the EDP. So as long as those forces are present, there will be a charge separation, and an electric field.

 

Inside the Earth, the threshold for EDP appears to be achieved at the Moho, meaning that the upper mantle is positively charged, and the crust is negatively charged. Note that this threshold is dependent on the hydrostatic pressure, as well as the ionization potential of the chemicals. If gravitational loading were the only factor, the Moho would be an isobar, which it is not. But neither does it follow the lines of chemical differentiation, which are abrupt and irregular.^22:77 Only a combination of gravitational loading and ionization potential can produce the observed variability in the depth of the Moho.²³ Since the oceanic basalts have higher concentrations of heavy elements than the continental granites, they are more easily ionized, and thus the threshold for EDP is achieved with less gravitational loading. So the Moho is only ~6 km below the ocean floor (i.e., ~10 km below sea level), while the Moho occurs at ~35 km below the surface of the continents.

 

If the gravitational loading remained constant, the forced ionization would be static, and there wouldn't be any electric currents responding to the electric field between the mantle and the crust — they would be true "current-free double-layers" (CFDLs). But crustal deformation alters the pressure at depth. For example, if the crust buckles because of lateral pressure, the buckle relieves the gravitational loading on the underlying rock, since the lateral compression strength of the plate carries the weight, like a Roman arch. The reduction in gravitational loading allows electrons to flow back into the mantle that had been forcibly ionized. Thus an electric current has been generated. The effect is far more dramatic than tidal deformation, which elevates the crust as much as 1.11 m at high tide, while pre-quake buckling can raise the surface several meters in just a couple of days. So the resulting electric current will be much stronger than normal.

 

Note that it seems odd to be talking about electric currents in rocks. Solid granite has a resistance of 2.4 MΩ, and the electric field necessary to get a powerful current flowing against such resistance just isn't present. But the fracturing in the buckled crust makes it a much better conductor. A crack only 1 nm wide is enough to allow the passage of electrons, and the resistance drops to roughly 377 ohms, enabling currents at much lower voltages.^1:71,24,25

 

So what ultimately causes the earthquake?

 

It is commonly believed that the buckled crust is elastic. If that were true, it would be able to store energy that could be released catastrophically when the traction failed along the fault. But that isn't correct — under stresses sufficient to cause buckling, the rigid crust fractures, which is an irreversible deformation that stores no energy.^14:39 Without elasticity, a buckled crust shouldn't produce an earthquake — the buckle should just become a permanent geologic feature, possibly growing over a long period of time into something resembling the Appalachian Mountains. Some have argued that the uplifted rock has converted pressure into gravitational potential that gets released catastrophically. But if gravity were powerful enough to generate a megathrust fault just because the crust was elevated a few meters, mountain ranges 5 km high, within 250 km of a trench (and fully inside the Benioff zone²⁶) more than 5 km deep, would be quite impossible, since 10 km of gravitational potential wouldn't allow it. (See Figure 6.)

 

 

Figure 6. Topographic profile, with an exaggerated vertical scale, through the Peru-Chile trench and Andes Mountains.

 

 

Since earthquakes definitely happen, and mountain ranges certainly exist, we can only conclude that the kinetic energy of colliding plates isn't stored and then released catastrophically, since there is no suitable storage mechanism. Rather, the plate collision can only be releasing some other form of potential.

 

And what other potentials are there? We know that electrostatic potentials are present, as a consequence of electron degeneracy pressure (EDP), and that there are distinctive changes in electric fields associated with earthquakes. So we should consider the possibility that the kinetic energy of the plates is somehow triggering the release of electrostatic potentials, by somehow altering the degree of EDP.

 

If we step through the whole process, we can easily see where this is happening.

1. Plate movement builds up lateral pressure at the fault.
2. The rigid crust buckles under the lateral pressure.
3. The elevation of the crust reduces the gravitational loading underneath it.
4. The reduction in gravitational loading reduces the degree of ionization.
5. De-ionization motivates an electric current through the fractured crust.
6. The electric current causes ohmic heating in the crust.
7. The ohmic heating causes the crust to expand.
8. The expansion increases the buckle.

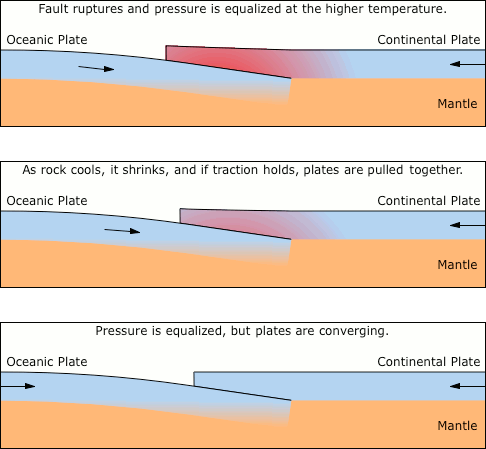
Note that steps 3~8 constitute a force feedback loop. The more the crust buckles, the more ohmic heating it gets, which causes it to expand, increasing the buckle. Also note that the buckle reduces the mating surface of the two plates, meaning less traction. (See in Figure 7.) A runaway expansion of the crust, coupled with a loss of traction, guarantees a rupture.

 

 

Figure 7. Subduction fault.

 

 

The one other factor that increases the chance of an earthquake is high tide and a new moon, when the tidal forces are the greatest.^27,28 In the standard model, this doesn't make sense, since gravity pulling on the crustal buckle should relieve stress at the fault, and the quake should wait for low tide and a moon in its 1^st or 3^rd quarter. But if tidal forces increase the crustal buckle, they are contributing to the force feedback loop that causes the runaway expansion of the crust.

 

This model passes the next test as well. One of the major mysteries about earthquakes is that they produce a series of waves, sometimes lasting for minutes. The inelastic rock shouldn't oscillate like this. As proof, an experiment was once conducted, involving the detonation of a 1 megaton nuclear bomb, 1 km below the surface. This successfully caused a surface fault about 1.2 km long. But it did not create a series of seismic waves. The second wave had only a small fraction of the energy of the initial shock front, and the elastic reverberations died out quite quickly.²⁹ Without elasticity, what causes repetitive seismic waves?

 

In an EM context, we'd call this a form of sputtering. The electric currents flowing through microfractures turn them into plasma discharge channels. These can get very hot, very fast, and the pressure can quickly become enormous, and this is the force that ultimately causes the rupture. (In other words, with its low thermal conductivity, the crust is not subjected to general ohmic heating, resulting in expansion. Rather, extreme heat in micro-channels generates the hydrostatic pressure.) The amount of force that this can generate should not be underestimated. Consider the following report of what one lightning strike did to a large chunk of rock.^30:150,31:72

In Fetlar, one of the Shetland Islands, a solid mass of rock 32.0 m long, 3.0 m broad, and in some places more than 1.2 m high, was in an instant torn from its bed by lightning and broken into three large and several small fragments... [One fragment], 8.5 m long, 5.2 m broad, and 1.5 m in thickness, was hurled across a high point of rock to a distance of 46 m. Another broken mass, about 12.2 m long, was thrown still farther, but in the same direction, and quite into the sea..."

This is an unusual occurrence, and understandably so, considering the normal resistance of granite. Clearly the discharge found its way through the rock by following fractures. And though there is no theoretical limit to the amount of ohmic heating that can be applied to matter, there is little back-pressure on the current — conductivity increases with temperature. Once the current found a way through the rock, the current and the pressure on the surrounding rock increased together, eventually exceeding the tensile strength of the rock.

 

The conditions are different deep inside the Earth, where the discharges are self-defeating, because the expansion of the heated rock closes the channels, raising the resistance back up to 2.4 MΩ. Yet slippage at the fault sends a negative pressure wave back through the rock. This means that discharge channels closed by increasing pressure are re-opened. So the current flows again, quickly restoring the temperatures and pressures necessary for another rupture. The result is a series of shock waves that can sometimes last for minutes. But these are not elastic reverberations. Rather, each shock wave has its own electro-mechanical source. Successive sputtering then eventually relieves all of the pressure. When we inspect the fault, we see that the subduction has advanced another couple of meters. But there was actually a series of ruptures only centimeters apiece, from each individual wave.

 

Now we should consider the behaviors of this model after the quake. All of the pressure at the fault has been relieved, and the continental plate lies back down on the oceanic plate, re-establishing traction. Then the hot rock begins to cool. As it does, it shrinks. There are two possible consequences of the shrinkage.

 

First, if the traction fails, there will be an aftershock. Note that a number of laws have been empirically derived from the regularity of aftershock swarms.

• Omori's law: aftershock frequency varies with the inverse of the time after the main shock.³²
• Båth's law: the difference in magnitude between a main shock and its largest aftershock is approximately 1.1~1.2 MMS, regardless of the main shock magnitude.³³ So if the main shock is M7.5, the largest aftershock will be M6.3~6.4.
• Gutenberg-Richter law: there are fewer large aftershocks, and more small ones.^34:69

Other models seem to be consistent with these laws, but they assume elasticity that granites and basalts don't have. In the present model, these laws are predictable consequences of post-rupture shrinkage in an inelastic medium. Heat dissipation is fast at first, and asymptotically approaches zero with time. Hence aftershocks will be frequent right after the main quake, and the rate will slow asymptotically (i.e., Omori's law). The energy of the largest aftershock will be a fixed amount less than the main shock, because quake magnitudes are measured on a log scale, and cooling per degree of difference also follows a log scale. Hence a large rupture will be hot, and will cool rapidly, with massive shrinkage, while a small rupture is produced by a smaller temperature difference, and the shrinkage will be consistently less (i.e., Båth's law). And shrinkage of a large block can easily produce many more small ruptures than large ones (i.e., Gutenberg-Richter law). In the conventional model, only considering tectonic pressure and the release thereof, and acknowledging the inelasticity of the granite/basalt, both plates should move as rigid units, and ruptures should only occur when the traction fails along the entire fault. But stresses vary in a shrinking plate, being the product of local and compounded distant shrinkage, and there are many more opportunities for small ruptures than for large ones.

 

Second, if the traction holds, the shrinkage will produce a tensile force on both plates, pulling them together. (See Figure 8.) Now if we just acknowledge that the force feedback loop that causes the rupture happens fast, while the cooling happens slowly, we see that the plates are subjected to tensile force longer than they are under pressure. For this reason, more of the tensile force gets converted to momenta than the collisional pressure detracts from it. In short, the net force is a pull, and the entire process is a form of ratcheting.

 

 

Figure 8. Post-rupture shrinkage pulls the plates together.

 

 

As such, we might now have an answer to the original question concerning what causes plate motion in the first place. It isn't pressure at the mid-ocean ridges, and it isn't the negative buoyancy of the oceanic crust that gets subducted. Nor is tidal deformation powerful enough to shift crustal plates, given that the force was focused in just the right place, which it isn't. But a net tensile force on the plates will certainly contribute to plate motion, and might be the prime mover.

 

As such, a couple of questions need to be answered.

 

First, granite/basalt is high in compression strength, but low in tensile strength. Could a tensile force at a plate boundary actually drag an entire continent toward the fault zone?

 

This is a problem for any theory that states that the continents are being pulled apart, instead of pushed together (including the crustal convection model). Either way, it's an excellent question. And there is certainly evidence of the crustal tensile strength failing. Rifts such as in Death Valley USA, and possibly in back-arc basins, result from stretching near subduction zones. (See Figure 9.) Problematic for the crustal convection model is that it isn't the oceanic crust that is getting stretched — the rifts occur in the continental crust, which shouldn't be under any tensile strain at all in that model. In the present model, the rifts occur in the continental crust because it is under tensile strain too, and because it got fractured by crustal buckling prior to the quake.

 

 

Figure 9. Rifts form due to crustal stretching.

 

 

Nevertheless, the mid-ocean ridges are proof that continental spreading begins there, begging the question of why the rifts don't occur throughout the continental crust. The most likely overall explanation is that it isn't a tensile force per se, and it's not just the crust that's involved. Rather, high pressure in the lower lithosphere, due to vertical loading, is relieved at one end by subduction, and the rest of the lithosphere flows in that direction, dragging the crust along with it. So it's really just an absence of a compression force, combined with the plasticity below the crust, that moves the plates.

 

Second, a question specific to plate ratcheting concerns how the process was initiated. If the plates have collisional momentum, there will be a rupture, and when the plates fuse back together, shrinkage will supply the tensile force (or the absence of compression at depth) that replenishes the momentum, eventually leading to the next rupture. But how did the plates develop collisional momentum before the first quake? There are a variety of possibilities, but one candidate is the "shock dynamics" model, which asserts that an impact event at the northern tip of Madagascar set the plates in motion.³⁵ This model explains so many details about plate movements that it's an excellent place to start. But an instantaneous event would not create the features that could have only emerged after a long period of time, such as magnetic striping on the seafloors centered on the mid-ocean ridges.*¹⁵⁷¹² So it's more likely that an impact event initiated plate motions, but thereafter, plate ratcheting perpetuates the process.

 

Another large-scale issue that needs to be addressed is deep-focus quakes (i.e., with hypocenters as deep as 700 km). This "should" be impossible, as the rock below ~40 km is under sufficient pressure to flow. (In the present model, it's not just pressure all by itself that enables the plasticity, but more importantly, the ionization, which weakens the crystal lattice.) The significance is that such rock shouldn't be capable of rupturing.³⁶ For this reason, the consensus is that a subducted plate is sent diving down into the mantle, and because it is brittle, it is still capable of rupturing, until it is heated up to the same temperature as the rest of the mantle. (See Figure 10 for a graphic depicting the standard model of deep focus quakes.)

 

The thermal conductivity of granite might be poor, but subduction at a rate of less than 10 cm/yr means that it takes more than 7,000,000 years to get to a depth of 700 km. Granite isn't that poor of a thermal conductor. It's also hard to believe that the subducted plate would encounter enough friction for a rupture. So other mechanisms have been proposed for deep seismogenesis, such as the dewatering of the crust as it heats up, with its resultant effect on the rigidity of the subducted plate. But none of the models have explained how the crust, only 6 km thick and heavily fractured from the down-turn at the continental margin, could be pushed (or pulled for that matter) 700 km into the mantle without folding (or "rifting" if it's being pulled). So the universally planar nature of Benioff zones has proved an intractable problem for subduction models.

 

The present model offers another suggestion. Buckling of the crust can affect the pressure theoretically all of the way to the core (though the difference will relax with the square of the distance from the buckle). The increase before the quake, and the sudden decrease during the quake, will reduce/increase hydrostatic pressure at depth, causing electron uptake/expulsion. Either way, electric currents are pushed through micro-cracks in the rocks. Hence rock at a depth of 700 km might be too plastic for a rupture, but it might still be vulnerable to the explosive effects of electric currents that get triggered by sudden changes in pressure. The double Benioff zones, which appear to be ubiquitous,³⁷ are then explained as the same phenomenon, but acting on different degrees of ionization in the mantle. This is common in electrostatics — if an electric field is suddenly altered, the effect will appear in equidistant shells, one where neutral matter went to the first degree of ionization, another where matter that was already ionized got stepped up to the next degree, etc.

 

Note that not all geologists believe that the lithosphere drifts across the asthenosphere, since mountain ranges near subduction zones appear to have "roots" as deep as 600 km.^1:50,38 Such "roots" are detected as wave transmission speed anomalies, which imply some sort of continuous structure. But if this is true, both the lithosphere and asthenosphere are moving, and the amount of energy to accomplish that amount of deformation simply isn't present. It seems more reasonable to think that the mountain "roots" are not physical structures, but rather, some sort of transient condition that occurs under the weight of the mountains, and which moves with the mountains. For example, the transmission speed anomalies might define the limits of an extra degree of EDP due to the weight of the mountains. Deep-focus earthquakes are then occurring along an ionization boundary, not a fault. The oceanic crust might then simply slip under the continental crust with a lot less energy, and never extend far into the lithosphere before melting and merging with the existing magma there.

 

Another type of data that can be assimilated is gravity anomalies. Upward crustal buckling results in a reduction of the gravity field, as detected by satellites, and by ground-based instrumentation up to hundreds of kilometers away.^39,40,41 This is odd because bringing the crust closer to the satellite should increase the gravity field. Likewise, if lateral pressure compacts matter just prior to a rupture, the expectation would be an increase in gravity field, not a decrease. So there has to be more to it than just gravity. In the present thesis, crustal buckling generates powerful electric fields inside the Earth, with a reduction in the net negative charge at the surface. The consequence of this is a diminished positive charge density in the ionosphere. If the satellites are negatively charged, due to electron bombardment in space, they will be attracted to the positive ionosphere, and less so if the charge density drops, resulting in a "gravity anomaly".

 

So far, the present model has addressed the salient properties of quakes. It can be further tested by reviewing a list of anomalies that have been observed (and sometimes quantified) over the years, as cataloged by a noted authority on quakes.^14:38 Nested under each bullet point is the present model's interpretation.

• changing well water levels
  • The crust is buckling under lateral pressure.
• ground-hugging fog
  • The buckling creates a low pressure under it, which cancels EDP. So electrons flow downward. This produces a temporary electron deficit in the overlying rock. Hence the Earth, at its surface, becomes positively charged.^14:38,42:402 A negative space charge develops in the air above the ground. Electric fields encourage the condensation of water molecules (by polarizing them). The fields also cool the air, because the electric force removes degrees of freedom.⁴³ So the conditions favor the production of water aerosols, which will be negatively charged, and which will cling tightly to the positive charge in the ground.
• earthquake lights from ridges and mountain tops⁴⁴
  • The electric field exceeds the potential for corona discharges from pointy objects (or even large geologic features).
• low frequency electromagnetic emission
  • Ohmic heating generates infrared radiation.
• local magnetic field anomalies up to 0.5% of the Earth's dipole field
  • Electric currents generate magnetic fields. The piezo effect does not.
• temperature anomalies by several degrees over wide areas as seen in satellite images
  • Ohmic heating again.
• changes in the elevation of the Earth's surface
  • The Earth is buckling.
• changes in the plasma density of the ionosphere
  • If the Earth is positively charged, that's a polarity reversal from the fair weather field, which will affect the ionosphere.

In conclusion, the present model appears to be consistent with a wide range of quake-related phenomena, and therefore appears to be worthy of further investigation.

 

Re: Magnetic Striping

Clarification