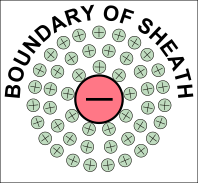
© Charles Chandler

 

Figure 1. Titus-Bode Law

The Titius-Bode Law encapsulates the observation that all of the planets out to Uranus have orbits around the Sun that are twice the radius of the previous planet. (See Figure 1.) This leaves a large gap between Mars & Jupiter, but that's precisely where we find the Asteroid Belt, with Ceres as its largest member. Heinrich Olbers suggested in 1802 that Ceres used to be a much larger planet following the law, though it was shattered by an impact, leaving the asteroids as remnants.

 

There have been many attempts to explain the Titius-Bode Law in Newtonian terms. The most common is a negative argument — it isn't that anything is forcing the planets into specific orbits — rather, planets not adequately spaced from each other will have their orbits perturbed, and only the orbits free from such interference have persisted. But this begs the question of what happened to the planets whose orbits were perturbed — they should still be a part of the solar system, just in highly elliptical orbits.

 

A possibility not previously considered is that the planets are actually locked into specific orbits by two opposing forces, with gravity pulling inward, and with electrostatic repulsion pushing back out. This idea was developed in the section on Accretion, to explain a similar phenomenon at a smaller scale — dusty plasmas don't tend to collapse into stars under their own weight, constituting evidence of a force opposing gravity, which was shown to be electrostatic. The Debye cells that make up a dusty plasma, with their negatively charged nuclei and positively charged sheaths, show net positive charges at a distance, due to the proximity of the near sides of the positively charged sheaths to a distant test charge, and due to the inverse square law. It follows that two Debye cells, both showing net positive charges at a distance, will show a net electrostatic repulsion between them.^1,2,3 (See Figure 2.)

 

 

		← net repulsion →
Figure 2. The sheaths of neighboring Debye cells produce a net repulsion between the cells, because of the inverse square law.

 

 

With a typical center-to-center spacing of 10 m between Debye cells, if there is just 1 ion per 10¹⁵ neutral atoms, the electrostatic repulsion is as strong as the gravitational attraction. At greater degrees of ionization or at closer spacings, the repulsion is stronger, preventing the gravitational collapse.

 

Table 1. Planetary Distance/Diameter Ratios planets spacing ave. diam. dist/diam Mercury, Venus 5.03 × 1010 8.49 × 106 5.92 × 103 Venus, Earth 4.14 × 1010 1.24 × 107 3.33 × 103 Earth, Mars 7.83 × 1010 9.76 × 106 8.03 × 103 Mars, Jupiter 5.51 × 1011 7.33 × 107 7.51 × 103 Jupiter, Saturn 6.55 × 1011 1.27 × 108 5.15 × 103 Saturn, Uranus 1.44 × 1012 8.26 × 107 1.75 × 104 Uranus, Neptune 1.63 × 1012 4.98 × 107 3.27 × 104 Neptune, Pluto 1.37 × 1012 2.57 × 107 5.33 × 104

This is interesting because planets have the same electrostatic configuration, being negatively charged, surrounded by positively charged atmospheres (including the interplanetary medium). The spacing between the planets is roughly the same spacing as in dusty plasmas. The dust grain in a Debye cell typically has a diameter of roughly 10⁻⁴ m. With a typical distance of 10 m between cells, that's a distance/diameter ratio of 10⁵. The ratio between the planets is within two orders of magnitude of this. (See Table 1.)

 

The fact that the planets are packed tighter than typical Debye cells is easily explained by the presence of the Sun's gravity, which is an extra consolidating force that isn't present in a dusty plasma. The twofold increase in separation with distance from the Sun is explained as the diminishing effect of the Sun's gravity with distance from it. In other words, the outer planets are not packed as tightly, because the packing force is weaker. After Uranus, the orbits of Neptune and Pluto deviate from the Titius-Bode Law, and an understanding of why will complete the concept. The orbits are not asymptotically approaching infinity at planet #27 (or whatever) — they're asymptotically approaching the distance/diameter ratio of 10⁵, which is what they would be in free space, without gravity from much larger objects nearby, such as the Sun, Jupiter, and Saturn.

 

The same distance/diameter ratio shows up at the next higher scale — the radius of the heliosphere is 2.16 × 10⁴ times that of the Sun, suggesting that the solar system, taken as a whole, is like one big Debye cell.

 

Table 2. Dist/Diam in Globular Clusters density spacing ave. diam. dist/diam minimum 1.23 × 1013 1.39 × 109 8.87 × 103 average 1.23 × 1016 1.39 × 109 8.87 × 106

Figure 3. NGC 2808

And this same distance/diameter ratio shows up yet again at the next higher scale, in the spacing of stellar systems in globular clusters (as in Figure 3). These are gravitationally bound clumps of stars on the fringes of galaxies, making them relatively isolated systems responding only to local forces. And these clumps have had a long time to come into equilibrium. Most of the stars are at the same stage of evolution on the Hertzsprung-Russell diagram,⁴ meaning that they formed at roughly the same time. There is very little interstellar dust, leaving no material for new star formation. And the stars that are there are very old — typically 10 billion years old, and some seeming to be older than Big Bang cosmology allows.⁵ Furthermore, globular clusters are dominated by Populaton II stars, made of mainly hydrogen & helium, and little in the way of heavier elements from previous stellar cycles. So these stars formed very early, and haven't changed since. Given all of that time, why haven't these clusters undergone gravitational collapse, despite being much more dense than the distribution of stars within galaxies? The only possible answer is that something is opposing the collapse. It isn't hydrostatic pressure, since there is very little interstellar plasma in globular clusters. It isn't centrifugal force, since the clusters don't rotate. The remaining possibility is electrostatic repulsion. And the spacing between the stars is roughly the same as the spacing of Debye cells in a dusty plasma. Given that the average spacing is 0.4 parsecs (1.23 × 10¹⁶ m),⁶ and if we assume that the average diameter of the stars is the same as the Sun's (1.39 × 10⁹ m), that's a ratio of 8.87 × 10⁶. This is almost two orders of magnitude higher than the ratio of 10⁵ that is typical for Debye cells in dusty plasmas. But this is easily possible if the degree of ionization is greater than the 1 charged particle in 10¹⁵ neutrals calculated in the section on Accretion. The minimum is two orders of magnitude more dense than 10⁵, because of gravitational loading, similar to the compression of planetary orbits in the inner solar system.

 

The universality of this principle is supported by recent findings that it holds for planetary systems other than our own.⁷ 909 planets in 355 multi-planet systems were studied, and the correlation was beyond chance.

 

Table 3. Dist/Diam in Molecules element spacing nuc. diam. dist/diam Hydrogen 7.41 × 10−11 3.50 × 10−15 2.12 × 104 Carbon 1.43 × 10−10 4.62 × 10−15 3.08 × 104 Oxygen 1.21 × 10−10 5.07 × 10−15 2.38 × 104 Gold 2.88 × 10−10 2.10 × 10−14 1.37 × 104 Uranium 2.77 × 10−10 2.39 × 10−14 1.16 × 104

And if we go in the other direction, to the smallest scale on which the electric force operates, we find the same ratio. The spacing between the atoms in elementary molecules is well known, due to the characteristic wavelengths that such molecules can absorb.^8,9 Then the radii of atomic nuclei are between 1.75 × 10⁻¹⁵ to 1.50 × 10⁻¹⁴ m.^10,11 The resulting distance/diameter ratios are a fairly consistent 10⁴, despite the rather dramatic differences in bonds for the various elements. This suggests that the distance between the nuclei is being set by the balance between attraction & repulsion — if the nuclei get too close, the repulsion between the like-charged nuclei pushes them apart, while at greater distances, the attraction to the shared electrons dominates.

 

Calculations