© Charles Chandler
Figure 1. Charge Separation Under Pressure
At left is an abstract representation of a normal crystal lattice, using the familiar icon for an atom, and showing connections of electron shells. At right, extreme pressure has forced the expulsion of one of the electrons from the atom in the center. The expelled electron is to be found just outside, wherever there is room for it, while attracted to the positive ion by the electric force.
Electron Degeneracy Pressure
$$P=\frac{h^2}{20m_em_p^{5/3}}\left(\frac{3}{\pi}\right)^{2/3}\left(\frac{\rho}{\mu_e}\right)^{5/3}$$ where: P = pressure h = Planck's constant me = mp = ρ = density μe = electron/proton ratio Thus the Pauli Exclusion Principle holds even for supercritical fluids. Monoatomic matter above the critical point isn't constrained by covalent bonds. But when two atoms are forcibly pushed together, the first conflict will be between the outer electrons. If the pressure is greater than the ionization potential of the atoms, the conflict results in the expulsion of electrons, leaving a strong electrostatic repulsion between the positively charged atomic nuclei, and further compression has to fight the Coulomb force. This marks the transition from compressibility to elasticity, which is very different. The Quantum Mechanics term for this effect is electron degeneracy pressure (EDP), though the Pauli Exclusion Principle predated QM, and is not reliant on it.If the pressure is coming from gravitational loading, it increases with depth, meaning greater compression, and atoms packed closer together. At the threshold for EDP, electrons are expelled, and they have nowhere to go but up, where they will find room between atoms that aren't as tightly packed. Thus the expelled electrons are forced to a higher altitude, leaving positive ions below.The implication not typically considered is that a charge separation has occurred, creating current-free double-layers (CFDLs) — they are layers of opposite charges, with a powerful electric field between them, but there is no current responding to the field, because something prevents it. Usually a sustained charge separation requires an insulator, but in this case, EDP separates the charges and keeps them separate. And gravity is forcing the EDP. So as long as those forces are present, there will be a charge separation, and an electric field.
1. Saumon, D.; Chabrier, G. (1992): Fluid hydrogen at high density: Pressure ionization. Physical Review A, 46 (4): 2084-2100 ⇧
2. Dyson, F. J.; Lenard, A. (1967): Stability of Matter. I. Journal of Mathematical Physics, 8 (3): 423-434 ⇧
3. Lenard, A.; Dyson, F. J. (1968): Stability of Matter. II. Journal of Mathematical Physics, 9 (5): 698-711 ⇧
4. Dyson, F. J. (1967): Ground‐State Energy of a Finite System of Charged Particles. Journal of Mathematical Physics, 8 (8): 1538-1545 ⇧
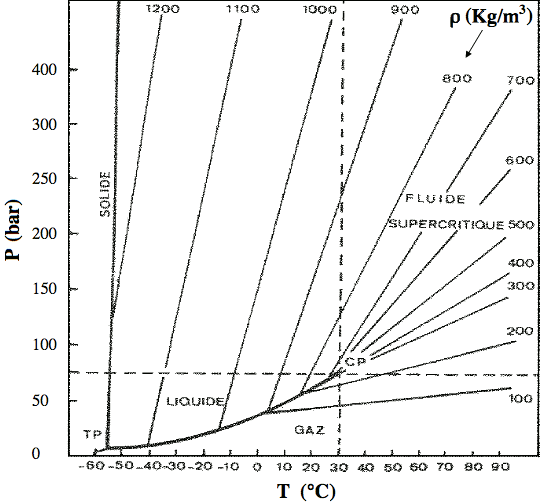
5. Otles, S. (2016): Supercritical Fluids — Density Considerations. ⇧
6. Tosatti, E. et al. (2009): High-pressure polymeric phases of carbon dioxide. Proceedings of the National Academy of Sciences, 106 (15): 6077-6081 ⇧
7. Weill, F. et al. (1999): Supercritical fluid processing: a new route for materials synthesis. Journal of Materials Chemistry, 9 (1): 67-75 ⇧