© Charles Chandler

 

Abstract

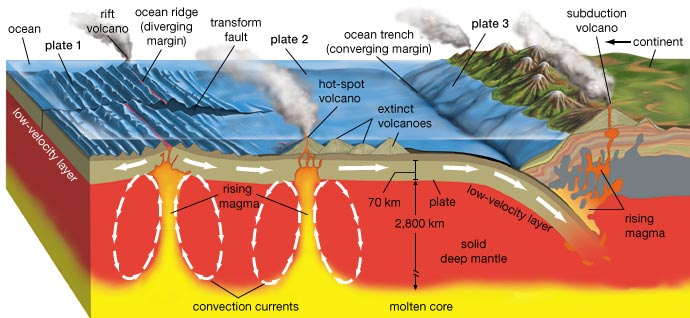
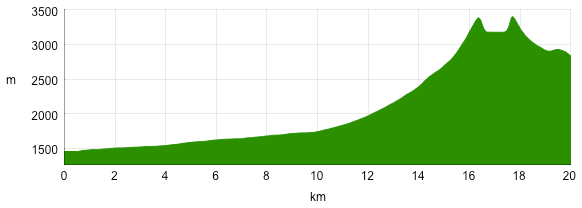
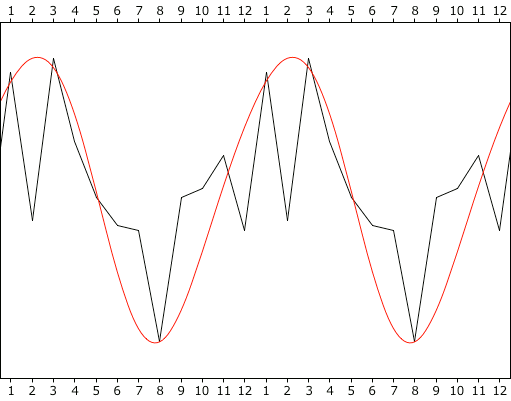
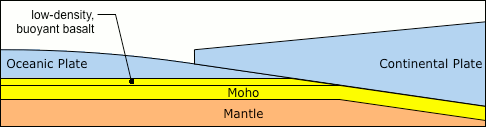
Fundamental inadequacies in our current understanding of volcanoes are explored. Felsic magma somehow finds its way through the thickest aspect of the crust (i.e., through mountain roots), forming subduction volcanoes at the surface, but the heat source that keeps the magma molten as it melts its way through solid rock hasn't been identified. And while mafic magma such as at Kīlauea flows through the much thinner oceanic crust, this has been explained as the outflow from a mantle plume, even though the Hawaiian-Emporer seamount chain began in a subduction zone that is older than the postulated plume, and which is mutually exclusive with it. Subduction volcanoes are therefore the primary riddle, and a new heat source is considered: resistive heating from telluric currents. Fractures due to crustal buckling in subduction zones enable such currents, which persist due to a positive feedback loop involving current density, resistive heating, and conductivity. The significance is that it might be possible to prevent cataclysmic eruptions, such as at Yellowstone, by shunting the current into a new path, using a conductive borehole some distance away from Yellowstone, which would remove the resistive heating and thereby relax the pressure in the existing chamber.

 

The standard model of volcanoes has mafic magma originating from mantle plumes (as in hot-spot volcanoes), and felsic magma bubbling up through the continental crust (as in subduction zone volcanoes). (See Figure 1.)

 

 

Figure 1. Standard model of geology.

© 2009 Mihai Andrei

 

 

Due to the distinct differences in composition, location, and behavior at the surface, mafic and felsic flows will be treated separately, starting with the latter.

 

When thinking of subducted matter bubbling up through the crust, we might imagine that this is just because hotter matter rises, which is true but irrelevant — the crystal lattice of the rigid crust doesn't permit convection. If a "thermal bubble" has risen through the crust, it can only be because it successfully melted its way through the crust. Yet in the process of doing this, it expends its thermal energy — as it heats the solid rock to the melting point, it itself gets cooled by the rock that it touches. Granite begins to melt at about 900 K, which is roughly the temperature in the Moho (i.e., 35 km below the continental surface, and the likely source of the magma).¹ For a thermal bubble to melt its way through 35 km of solid rock, it would have to stay hotter than 900 K the whole way, meaning that it had to start its ascent considerably hotter than 900 K (i.e., much hotter than its source).

 

Here the concept of a "mantle plume" could be invoked, which if accurate would allow some small portion of the Moho to be considerably hotter than 900 K, and therefore possess the thermal energy necessary to melt all of the way through 35 km of solid crust. But hot, high-pressure magma is a good thermal conductor. (In laboratory experiments at 1 ATM, it's a poor conductor, similar to wood.² But κ increases with temperature and with pressure.³) And in a good thermal conductor, concentrations of heat don't last long — the heat radiates rapidly into the surrounding matter. So if a plume did exist, it wouldn't melt a pin-prick hole through the crust — the heat would be distributed across of a vast area at the bottom of the crust, melting the entire mountain root system if it had the energy, and where the heat loss would be proportional to the difference in temperature, extinguishing the thermal anomaly. In other words, there is no reason to believe than a thermal bubble would remain adiabatic over a long period of time in a good thermal conductor, leaving the standard model without an explanation for the sustained concentration of heat in a subduction zone volcano.

 

Recent research has shown substantial increases in the electric conductivity of the Earth in the vicinity of magma chambers.⁴ This isn't terribly surprising, since magma is a much better electric conductor than solid rock. But there is a hidden significance to this — electric conductivity might enable another heat source. If there are electric currents flowing through the Earth, they will follow the path of least resistance (i.e., greatest conductivity). Then, the current will generate resistive heating in that conductor. Interestingly, hotter rock is a better electric conductor, especially above the melting point. So just a little bit of conductivity will attract all of the currents in the vicinity, and then resistive heating will increase the conductivity, which enables even more current. Thus a positive feedback loop has been instantiated. And this will create a concentration of heat, which is a requirement for a felsic eruption. So are there electric currents inside the Earth to generate resistive heating?

 

In a related paper on the Moho, it was established that tidal forces drive telluric currents.⁵ (When the crust is raised/lowered, the pressure at depth is decreased/increased, allowing/forcing electron uptake/liberation at depth, due to electron degeneracy pressure (EDP).⁶) At first glance, we wouldn't think that fluctuations in charge density at depth would drive currents all of the way through the crust. Solid granite has a resistance of 2.4 MΩ, and the electric field necessary to drive currents through such resistance just isn't present. But fractures in the buckled crust over a subduction zone make it a much better conductor. A crack only 1 nm wide is enough to allow the passage of electrons, and the resistance drops to roughly 377 ohms, enabling currents at much lower voltages.^7:71,8,9 Once a little bit of current starts flowing, the heat~conductivity feedback loop promotes the fracture to the preferred channel for all of the current in the vicinity. Once established, the discharge channel can propagate all of the way from the Moho to the surface, much the way lightning propagates through the atmosphere (but much, much slower).

 

This means that the magma that reaches the surface doesn't bubble all of the way up from the Moho, nor was it forced through cracks in the crust by the enormous pressure at depth. Rather, an electric current melts its way through the crust, and the eruption at the surface is just the spatter out of the top of the discharge channel.

 

In this context, the pressurization of the magma tube prior to an explosive eruption makes more sense. A thermal bubble melting its way to the surface is incapable of pressure greater than the surrounding rock, since it is all subject to the same gravitational loading. But with its own heat source, the magma tube can develop the excess pressure necessary to fracture the surrounding rock.

 

Of course, once the eruption begins, lava can be accelerated high into the air, but not because of the pre-rupture pressurization of the molten granite. Rather (as is conventionally acknowledged), it's because of gases trapped inside the magma.¹⁰ The gases (especially water vapor) are highly compressible, meaning that the magma is spring-loaded. When the pressure relaxes, the gases can expand, accelerating the lava out of the vent. This explains why high-velocity ejections can continue for the duration of the eruption, which wouldn't happen if it was just the release of pressure by the initial rupture.

 

Figure 2. Topographic profile through the lava lake (elevation: 3200 m) inside the caldera of Mount Nyiragongo (at right), down to Lake Kivu (at left).

Between episodic eruptions, some magma tubes stay molten, producing sustained lava lakes. Contained within caldera walls built by previous eruptions, the lava achieves its hydrostatic equilibrium, which is well above the average elevation in the vicinity. The best example of this is Mount Nyiragongo, which has the largest sustained lava lake in the world, at an elevation of roughly 3200 m, which is roughly 1700 m above the surrounding plains. (See Figure 2.) The lava lake has definitely achieved the hydrostatic equilibrium. But how could that be 1700 m above the plains, if it's all under the same gravitational loading?

 

The answer has to do with the expansion of matter with increasing temperature — the hotter magma is less dense than the surrounding solid rock, and therefore lighter, meaning that it takes a taller column of it to weigh the same as the solid rock. The thermal expansion coefficient for magma is 5.00 × 10⁻⁵ per K. From this we can calculate how deep the magma tube goes, given that it has expanded 1700 m more than the surrounding solid crust.

 

First we'll find the temperature difference between the magma and the crust. The magma is roughly 1500 K.^11,12,13 The surface of the crust is roughly 300 K, but the crust gets hotter with depth, so we can't just use the surface temperature. For now, we'll assume that the relevant depth is down to the Moho, which is roughly 900 K.¹⁴ So the average crustal temperature through the relevant depth is 600 K. This means that the magma is 1500 K − 600 K = 900 K hotter than the crust. 5.00 × 10⁻⁵ per K, times 900 K, equals a scale factor of 0.05. So we divide 1700 m (i.e., the height of the lava lake above the plain) by 0.05 to get the full depth of the magma tube. This comes out to 37.78 km. And seismology confirms that the depth of the Moho in that region (as measured from the nearest station in Kabale, Uganda) is 37.0 km.^15:74~75,78 This means that we used the right number for the average crustal temperature, and that the magma tube extends precisely to the Moho.

 

But there is no conventional explanation for the temperature of the lava lake persisting at 1200 K above the surface temperature, much less for it to be 600 K hotter than the Moho. If the magma originates at the Moho, it should start at that temperature, and cool as it rises, with the relaxing pressure, and with the surrounding solid rock absorbing heat. That can only be evidence of another heat source, which can only be resistive heating from electric currents flowing through the magma, since it is the only other available source, and since it is the only source that can create the required concentration of heat into a tubular form.

 

Figure 3. Number of volcanic eruptions per month, 1900~1999, and a 4^th order spline (with an exaggerated vertical scale). Maximum: 166 in February. Minimum: 105 in August. Data courtesy Smithsonian Institution.

To double-check this thesis, felsic eruptions should be more likely during winter (in the northern hemisphere), when the Earth is closer to the Sun, and thus the tidal forces are stronger (for the same reasons that earthquakes and the Seneca Guns occur at these times). And indeed, that's when felsic eruptions are the most likely to occur. (See Figure 3.) There is also evidence of the diurnal tidal cycle influencing eruptions and lava flows.^16,17

 

Another behavior of felsic eruptions that is troublesome for the Newtonian regime is their sporadic nature. It's common for there to be a small eruption, and then a day or two later, there might be a much bigger one. If it's just pressure from inside the Earth, there should only be one catastrophic failure — once the pressure is relieved, it shouldn't be possible to have a secondary eruption, much less a more powerful one.

 

Part of the answer might come from the action of water vapor that comes out of solution, as described above. An explosive eruption relaxes the pressure on the underlying magma, allowing more vapor to evaporate, thereby driving the secondary eruption. But there is another possibility. At the Moho, electron degeneracy pressure (EDP) expels electrons. When the driving pressure is relieved by the initial eruption, EDP can no longer maintain the charge separation at depth. Then electrons are pulled down to the +ions at depth that are no longer being forcibly ionized. The flow of electrons constitutes an electric current, with its attendant resistive heating. And the new heat source restores the pressure to the magma chamber, causing the secondary eruption. In other words, sputtering electric currents can cause episodic explosions. The implication is that the secondary eruptions could be predicted on the basis of magnetic fields generated by the electric currents. This could provide hours, or even days, of lead time, and might be the most reliable index in the most catastrophic cases.

 

Now we should consider the properties of mafic flows. Without crustal deformation near a subduction zone to open up cracks for electric currents, how can the so-called "hot-spot" volcanoes get established?

 

The best example of this type of volcano is Kīlauea, but we should note that the magma flow didn't start there. Rather, the Hawaiian-Emperor Seamount Chain began something like 81 million years ago, at the triple junction of the Ulakhan Fault, the Aleutian Trench, and the Kuril Trench. In other words, it started as a subduction zone volcano. But then it took a trip across the Pacific Basin to its present location, roughly in the center. In the "hot-spot" model, this indicates that the mantle plume has shifted. But this would have a temperature anomaly persisting for 81 million years in a good thermal conductor, and favoring the center of an oceanic basin where the radiative heat loss is the most efficient. These behaviors cannot be described in thermodynamic terms.

 

 

Figure 4. Hawaiian-Emperor Seamount Chain

 

 

Figure 5. Puddling of low-density magma under oceanic crust.

More recent research suggests that it isn't a small, vertical hot-spot, but rather, a thin, broad layer of low-viscosity magma under the crust that drives such volcanoes.^18,19 This is easy to understand in thermodynamic terms. Since the oceanic crust is thinner, and if the Moho is a continuous layer of molten rock just under the crust, we can expect the lighter components to puddle on the underside of the oceanic crust. (See Figure 5.) If a volcano gets established on the edge of that puddle (in the subduction zone), and taps into the Moho, the lowest-viscosity magma under the oceanic crust will dominate the flow. But just as the volcano pulls that magma toward it, an equal-but-opposite force pulls the volcano toward the source of the fluid. Thus the subduction volcano gets pulled out to sea, and ultimately to the center of the oceanic basin. And as long as the magma channel through the crust is hotter than the surrounding rock, it remains the preferred conduit for telluric currents. The resistive heating then keeps the channel open. So we can expect the mafic flows at the end of the Hawaiian Chain to continue, as long as tidal forces keep driving telluric currents. And we can expect the "hot-spot" not to move any more, having already found the center of the basin.

 

The other significant seamount chains also began in subduction zones, including the Louisville Chain (starting at the Tonga-Kermadec Trench), the Marshall Island Chain (beginning at the Marianna Trench), and the Nazca-Easter-Pitcairn-Tuamotus Chain (beginning at the Peru-Chile Trench). The standard model denies that mantle plumes and subduction zones are related, since the latter is supposed to be where cooler oceanic crust is convectively sinking, which wouldn't tend to happen on top of a hot-spot. Rather, the sinking crust should absorb the heat from the plume, extinguishing it instead of creating it. Furthermore, the divergence supposedly caused by mantle plumes is inconsistent with the convergence in subduction zones. Mantle plumes were invented as an explanation for "hot-spot" volcanoes, and yet the actual expectations of such a construct are opposite from the observations. Plumes aren't even consistent with the supposed "convection" in mid-ocean ridges, as depicted in Figure 1. Rather, the mid-ocean ridges are actually cooler (radiating less than 30 mW/m²) than subduction zones (radiating more than 150 mW/m²).^20,7:45,21 If we then acknowledge the implausibility of thermal anomalies of such magnitude, due to the thermal conductivity of the mantle, the plumes are unlikely, and the effects aren't just lacking — they're opposite from the expectations. The only logical conclusion is that mantle plumes simply don't exist. There is a heat source in the Moho, where tidal oscillations raise and lower the threshold for charge separation due to EDP, thereby driving electric currents 4 times a day. Some of that current can get shunted through the crust, if fractures in subduction zones allow it. Once the current is sufficiently consolidated in a magma tube, resistive heating keeps the conduit open, and the thermal expansion coefficient places the hydrostatic equilibrium above the average surface level. Thus a steady flow of magma is enabled. Then asymmetrical inflow to the bottom of the magma tube results in the volcano shifting toward the source of the magma. In the case of seamounts, that would be toward the center of the oceanic basin, which is the case for all of the significant chains.

 

Figure 6. Electrostatic discharge inside a volcanic plume at Kīlauea, HI, July 2008.

© 2008 Center for the Study of Volcanoes

This model also does a better job of explaining why lava is positively charged, and electrostatic discharges in volcanic plumes occur regularly. (See Figure 6.) This is typically attributed to triboelectricity. But magma is a good conductor, so we wouldn't expect much of a static charge. Furthermore, the magma is made of the same stuff as the solid rock in the lava dome, and similar chemical compositions brushing past each other don't produce triboelectric charging. But if the release of pressure due to the rupture enables charge recombination at depth, electrons will flow downward, leaving the top end of the flow positively charged.

 

The implications of this thesis go way beyond just better volcano prediction. Consider the worst case scenario: the Yellowstone Supervolcano. We know that the pressure in the magma chamber is increasing, because we can measure the surface deformation from the expansion.²² If it continues, it's just a matter of time before it will erupt. When it does, it will constitute a mass extinction event due to the effects of the ash cloud. Is there anything that we can do to prevent this? We certainly shouldn't try drilling a borehole into the chamber to relieve the pressure, because that would simply cause that which we would like to prevent. But what if it is resistive heating from telluric currents that is enabling the magma to eat its way to the surface? That gives us a way of stopping it. All we have to do is go about 100 km away from Yellowstone, and drill a borehole 5~7 km into the crust. The drill, and the ground water surrounding it, are excellent conductors. Now all of the telluric currents in the area will prefer that channel, instead of having to force their way through another 5 km of solid crust at Yellowstone. With the currents flowing through our new borehole, instead of through the magma chamber at Yellowstone, the resistive heating is where we want it, and not where we don't want it. So the magma chamber at Yellowstone will start to cool, and will eventually freeze up.

 

What if the rock at the base of our borehole starts to melt? Who cares? With an open pipe all of the way to the surface, the magma can flow if it wants, but it will never develop any pressure inside an open pipe. What if this lightning rod eventually attracts enough current to melt all of the way to the Moho? Who cares? If the pipe is open all of the way to the surface, there won't be a catastrophic eruption, because the magma never had a chance to build up any pressure. Worst case scenario would be the formation of a new Kīlauea in the middle of the Rocky Mountains.

 

The cost of drilling a borehole varies depending on the conditions, from 1 to 4 million dollars per kilometer.²³ So a high-end estimate would be $20 million for a 5 km hole. As such, this is the most economical proposal for the prevention of a mass extinction event, of any kind.

 

Code: Nyiragongo Equilibrium