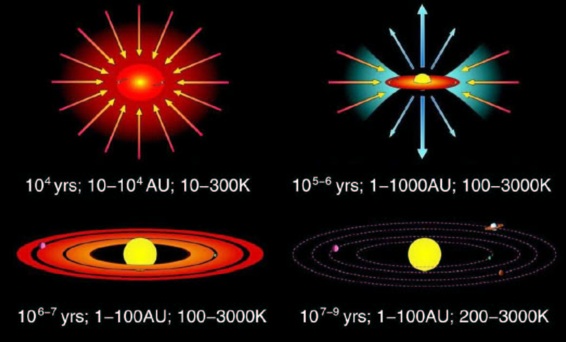
© Charles Chandler

 

In the standard model, the Sun formed from an accretion disc, and the planets congealed out of the left-overs. (See Figure 1.)

 

 

Figure 1. Standard model of stellar and planetary formation, credit Shu et al. (1987).

© 1987 NASA

 

 

The accretion disc model has its own problems, such as not being able to explain how the matter falling into the Sun gave up its angular momentum, especially as the net gravity approaches zero at the center of gravity, not to mention how the matter got compressed into a disc in the first place, this not being a form preferred by the Newtonian forces supposedly responsible. But even if those problems had solutions, there still wouldn't be an answer to why all planets (except Venus) have prograde rotations. If a strip of the accretion disc condensed into a planet, the net angular momentum would be retrograde. This is because the inner track orbits faster than the outer, such that its centrifugal force matches the greater gravity nearer the Sun. So all of the planets should spin in the opposite direction of their orbits. The standard model also does not explain why the planets are made of fundamentally different stuff compared to the interplanetary medium (IPM). While the IPM is mainly hydrogen, the planets are mainly heavy elements. Clearly these are products of fusion, but the pressure and temperature at the core of the Sun is supposedly just barely capable of fusing hydrogen into helium, and not capable of fusing helium into anything heavier. Inside the planets, the pressures and temperatures are nothing compared to inside the Sun, so even hydrogen fusion shouldn't be possible, begging the question of what fused the heavy elements out of the hydrogen in the IPM.

 

Such questions don't have answers in the standard model. Clearly there are forces at work far stronger than gravity, to overpower the hydrostatic pressure resisting the compression of the dusty plasma, and to fuse the heavy elements. So in no sense is a stellar system just a gravity vortex sucking matter into the central star — the matter had to have been rammed together by much stronger forces. The angular momentum is undeniable, but that doesn't mean that the progenitor had to have been a disc — it could have been two colliding linear filaments that did not meet perfectly head-on, and when they glanced off of each other, the angular momentum was created. In the CFDL model,¹ the electric force between alternately charged layers of plasma then bound the whole thing together, converting the excess hydrostatic potential to electrostatic potential. Of the total mass in the solar system, 99.9% of it is in the Sun, while all of the planets & moons put together only account for 0.1% of the total. So if the organizing charges only captured 99.9% of the matter, and left 0.1% of it in the heliosphere, we get planets. Still, the planets would have been formed at the same time, and in the same conditions as the Sun. Thus all of the planets would orbit the Sun in the same direction as its axial spin, because all of the matter had the same general angular momentum. And most of the planets would get prograde axial rotations for the same reason.

 

And at least some of the planets might have actually ignited into stars once formed.² Here we should note that there are many binary and even trinary stellar systems throughout the Universe, which wouldn't make sense if the only object that gets to be a star is whatever is at the center of the accretion disc. The fact that we don't see systems with more than three stars might just be because of the great distances separating us from them. If all of the planets in our solar system were stars too, the whole thing would still appear as a point source to our nearest neighbor outside of our solar system. If this is correct, the difference between a star and a planet is not a function of position within an accretion disc, but rather, it is a stage in an evolutionary process, wherein planets are simply further along. If so, the heavy elements were fused in situ during the stellar phase, and were not present in the primordial dusty plasma. In the late stage, the "stars" have lost their outer layers, and are now showing only their heavy-element cores.

 

Thus planetary science is rightfully an extension of stellar theory, not a totally different discipline. The most essential principle, identified in the section on the solar interior, concerns layers of alternating electric charge.

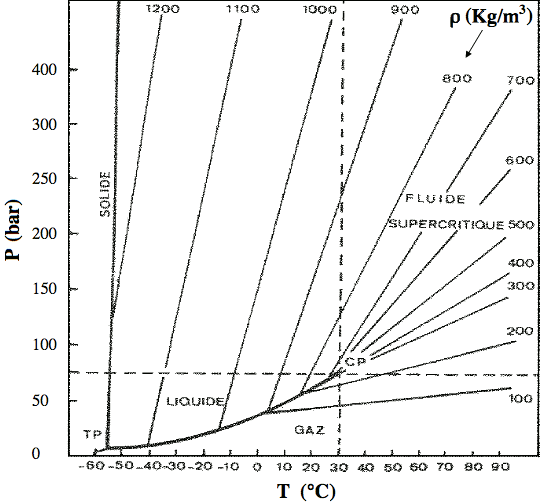
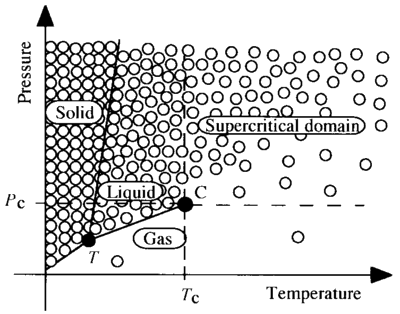
Figure 2. Charge Separation Under Pressure At left is an abstract representation of a normal crystal lattice, using the familiar icon for an atom, and showing connections of electron shells. At right, extreme pressure has forced the expulsion of one of the electrons from the atom in the center. The expelled electron is to be found just outside, wherever there is room for it, while attracted to the positive ion by the electric force.

It is well-known that at high pressures, matter gets ionized.³ This is because of the Pauli Exclusion Principle, whereby no two identical fermions (i.e., particles with half-integer spins, such as electrons) may simultaneously occupy the same quantum state in the same location. If atoms are pressed too close together, the electron shells of neighboring atoms overlap, and the conflict forces the liberation of one of the electrons. The extra force required to do this accounts for the incompressibility of liquids and solids.^4,5,6 (See Figure 2.)

 

The same is true even for supercritical fluids — even though they're too hot for crystal lattices, and thus have a plasticity uncharacteristic of their subcritical solid regimes, once compressed down to the density of a solid, they become just as incompressible as subcritical solids.^7,8 This fact isn't salient in the larger body of studies that have been done on supercritical fluids at less extreme pressures, and there's actually one place in the phase diagram where supercritical fluids are compressible beyond even the ideal gas laws — just above the critical temperature. (See the Nelson-Obert charts, and the closely spaced density lines just above the CP in Figure 3.) Nevertheless, the fluid is as incompressible as ever once it achieves its solid density. (See Figure 4.) CO₂ at its critical temperature of 31 °C, when subjected to 300 GPa (i.e., 3 million bars), has a density of 1400 kg/m³, which isn't much above its solid density below the triple point. So supercritical fluids still have a modulus of elasticity beginning at the solid density, but that isn't what we'd call compressibility, certainly not in line with the ideal gas laws.

 

 

Figure 3. Carbon dioxide phase diagram. © 2000 FutureChem

Figure 4. Another representation of the density of the various states.9 In the solid regime, increasing pressure doesn't further compress the matter — it simply enables the closest packed arrangement even at increasing temperatures.

 

 

Electron Degeneracy Pressure $$P=\frac{h^2}{20m_em_p^{5/3}}\left(\frac{3}{\pi}\right)^{2/3}\left(\frac{\rho}{\mu_e}\right)^{5/3}$$ where: P = pressure h = Planck's constant me = mass of electron mp = mass of proton ρ = density μe = electron/proton ratio

Thus the Pauli Exclusion Principle holds even for supercritical fluids. Monoatomic matter above the critical point isn't constrained by covalent bonds. But when two atoms are forcibly pushed together, the first conflict will be between the outer electrons. If the pressure is greater than the ionization potential of the atoms, the conflict results in the expulsion of electrons, leaving a strong electrostatic repulsion between the positively charged atomic nuclei, and further compression has to fight the Coulomb force. This marks the transition from compressibility to elasticity, which is very different. The Quantum Mechanics term for this effect is electron degeneracy pressure (EDP), though the Pauli Exclusion Principle predated QM, and is not reliant on it.

 

If the pressure is coming from gravitational loading, it increases with depth, meaning greater compression, and atoms packed closer together. At the threshold for EDP, electrons are expelled, and they have nowhere to go but up, where they will find room between atoms that aren't as tightly packed. Thus the expelled electrons are forced to a higher altitude, leaving positive ions below.

 

The implication not typically considered is that a charge separation has occurred, creating current-free double-layers (CFDLs) — they are layers of opposite charges, with a powerful electric field between them, but there is no current responding to the field, because something prevents it. Usually a sustained charge separation requires an insulator, but in this case, EDP separates the charges and keeps them separate. And gravity is forcing the EDP. So as long as those forces are present, there will be a charge separation, and an electric field.

 

Thus the pretext for the study of a planet is that the interior is separated into oppositely charged layers, bound tightly together by the electric force. Fluctuations in the pressure will then drive electric currents across the boundaries between these layers. (So the double-layers are not entirely current-free.) In the Sun, the energy released is obviously quite robust, while in planets, it is barely more than the ambient energy in the interplanetary medium. Nevertheless, CFDLs are the organizing principle, and disruptions in the layers are responsible for planetary dynamics, including earthquakes, volcanoes, climate change, etc.

 

How about a paper on Atmospheres?