© Charles Chandler

 

The resistance of a vacuum is commonly quoted as being infinite. Here's how Wikipedians put it...

Since a "perfect vacuum" contains no charged particles, it normally behaves as a perfect insulator. However, metal electrode surfaces can cause a region of the vacuum to become conductive by injecting free electrons or ions through either field electron emission or thermionic emission. Thermionic emission occurs when the thermal energy exceeds the metal's work function, while field electron emission occurs when the electric field at the surface of the metal is high enough to cause tunneling, which results in the ejection of free electrons from the metal into the vacuum. Externally heated electrodes are often used to generate an electron cloud as in the filament or indirectly heated cathode of vacuum tubes. Cold electrodes can also spontaneously produce electron clouds via thermionic emission when small incandescent regions (called cathode spots or anode spots) are formed. These are incandescent regions of the electrode surface that are created by a localized high current flow. These regions may be initiated by field electron emission, but are then sustained by localized thermionic emission once a vacuum arc forms. These small electron-emitting regions can form quite rapidly, even explosively, on a metal surface subjected to a high electrical field. Vacuum tubes and sprytrons are some of the electronic switching and amplifying devices based on vacuum conductivity.

So they start out saying that a perfect vacuum is a perfect insulator. Then they say that heat and/or electric field at the electrodes can liberate electrons, and then devices can utilize the resulting vacuum conductivity. Due to the legacy of shifts in EM theory as it evolved, such self-contradicting "explanations" are not uncommon. But the development of any fully mechanistic model incorporating EM requires an accurate definition of what EM actually is. The resistance of a vacuum has nothing to do with the electrode's work function, nor its ionization potential. The resistance of a vacuum, if it exists, is a property of the vacuum itself, and needs to be measured independent of the properties of the electrodes. In other words, the question is, "Once electrons are liberated from the crystal lattices in the electrodes, and are now moving through (otherwise) empty space, how much does the (otherwise) empty space impede the flow of electrons?" You can't measure the resistance of a vacuum by the heat and/or ionization potential of the electrodes, any more than you can measure the resistance of a copper wire by the properties of the contact posts feeding it the electricity — the issue is how much resistance is in the current-carrying medium itself. The electrodes have nothing to do with it.

 

The answer is that the vacuum doesn't impede the electrons at all. In a perfect vacuum (except for the test charge), the charged particle's behavior can be calculated by just three factors:

1. its mass, which gives it an inertial force that will resist acceleration,
2. its electric charge, which makes it responsive to an electric field, and
3. the strength of the electric field acting on the charged particle.

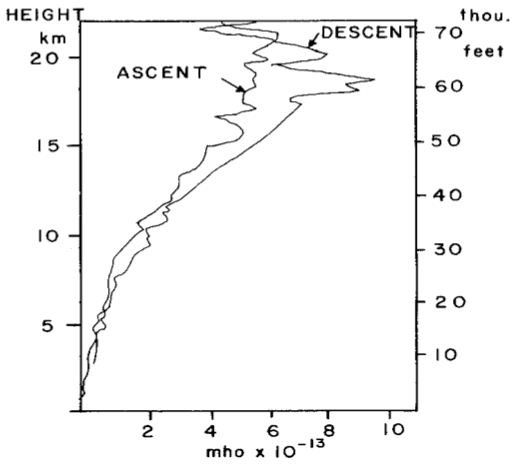
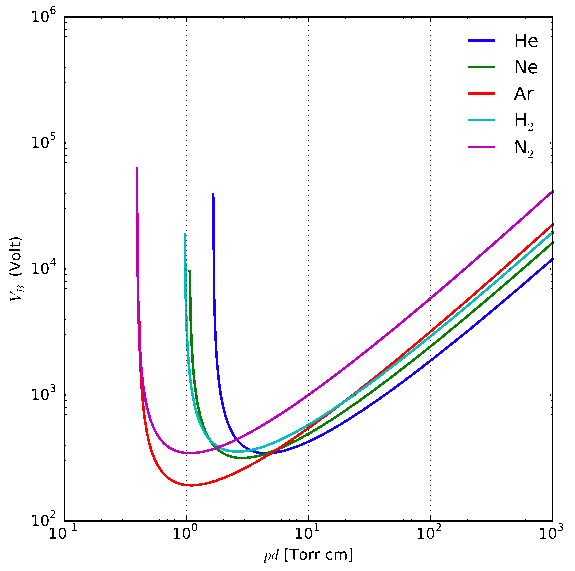
Then the acceleration of the particle is just the equilibrium between the inertial and electric forces.

 

In the real world, a perfect vacuum is impossible to achieve, and there will always be atoms floating around in the medium. Collisions with such atoms will always introduce resistance. This can be calculated if we know the resistance per collision, and the mean free path between collisions. The formulas for this are in a tutorial done at Georgia State University:

 

The current density (electric current per unit area, J=I/A) can be expressed in terms of the free electron density as:

 

Current Density from Free Electrons

J	=	nevd
where:
J	=	current density
n	=	free electron density
e	=	electric charge
vd	=	drift velocity

 

The number of atoms per unit volume (and the number free electrons for atoms like copper that have one free electron per atom) is:

 

Atoms per Volume

n	=	NAρ/A
where:
n	=	number of atoms
NA	=	Avogadro's number
ρ	=	density (kg / m3)
A	=	atomic mass (kg / mole)

 

From the standard form of Ohm's law and resistance in terms of resistivity:

 

Electric Resistance

R	=	ρL/A
where:
R	=	resistance (ohms)
ρ	=	resistivity
L	=	length
A	=	area

 

Electric Current

I	=	V / R
where:
I	=	current (amps)
V	=	potential (volts)
R	=	resistance (ohms)

 

Current Density from Volts & Ohms

J	=	V RA   =   V (ρLA)/A   =   EL ρL   =   E ρ   =   σE
where:
J	=	current density (joules)
V	=	electric field (volts)
R	=	resistance (ohms)
A	=	area (meters2)
ρ	=	resistivity
L	=	length (meters)
E	=	electric field
σ	=	conductivity

 

The next step is to relate the drift velocity to the electron speed, which can be approximated by the Fermi speed:

 

Fermi Speed

$$v_F = \sqrt{2E_F \over m}$$
where:
vF	=	Fermi speed
EF	=	electric field
m	=	mass

 

The drift speed can be expressed in terms of the accelerating electric field E, the electron mass, and the characteristic time between collisions.

 

Drift Velocity of Electron

vd	=	eE m τ = eE m d vF
where:
vd	=	drift velocity
e	=	charge of electron
E	=	electric field
m	=	mass of electron
τ	=	electromagnetic decay
d	=	distance between atoms
vF	=	Fermi speed

 

The conductivity of the material can be expressed in terms of the Fermi speed and the mean free path of an electron in the metal.

 

Conductivity

σ	=	ne2d mvF
where:
σ	=	conductivity
n	=	free electron density
e	=	charge of electron
d	=	distance between atoms
m	=	mass of electron
vF	=	Fermi speed

 

In other words, the raw speed of the electron is given just by the charge-to-mass ratio, while the net speed is the raw speed minus the time lost to collisions, which is a function of the mean free path. Hence a perfect vacuum, with an infinite mean free path, and therefore no time lost to collisions, has no resistance, and therefore, it's a perfect conductor.

 

This can be confirmed in many ways. For example, if a vacuum were a perfect insulator, neon lights wouldn't work. Electrons moving from one atom to another in a plasma are moving through empty space, which is the definition of a vacuum. If perfectly empty space presented infinite resistance, even a small mean free path would preclude any current at all, and electron transfer would only happen on particle collision. But then the electric current would travel through plasmas at no greater than the speed of sound. Since currents in plasmas actually travel at a respectable fraction of the speed of light, electrons are definitely moving through perfectly empty space, which they certainly wouldn't do if it were a perfect insulator. Here's where QM allows "tunneling" if the electric field exceeds the ionization potential of the electrodes. But if such "tunneling" always occurs if E exceeds the ionization potential, it isn't a property of the empty space — it's a property of the electrodes, and the enabling factors (E and the ionization potential) have already been identified. Thus the only tunneling is through the theoretical limits of QM, which wanted empty space to be a perfect insulator.

 

Another example demonstrates the direct relationship between increasing mean free path and increasing conductivity.^1:pg18 In the atmosphere, the air gets thinner with altitude, increasing the mean free path. At about 12 km above the surface, the density of the air is about 1/3 of that at the ground level. And as we can see in Figure 1, the conductivity at that height is 3 times that at the ground level.

 

 

Figure 1. Conductivity per altitude, as collected by a rocket-borne Gerdien cylinder, courtesy Lars Wåhlin.

 

 

So how did anybody ever think that empty space was an insulator? The confusion began with the discovery of Paschen's Law, before the underlying physics was understood. Again from Wikipedia...

Paschen's Law is an equation that gives the breakdown voltage (i.e., the voltage necessary to start a discharge or electric arc) between two electrodes in a gas as a function of pressure and gap length. It is named after Friedrich Paschen who discovered it empirically in 1889.

 

Paschen studied the breakdown voltage of various gases between parallel metal plates as the gas pressure and gap distance were varied. The voltage necessary to arc across the gap decreased as the pressure was reduced and then increased gradually, exceeding its original value. He also found that at normal pressure, the voltage needed to cause an arc reduced as the gap size was reduced but only to a point. As the gap was reduced further, the voltage required to cause an arc began to rise and again exceeded its original value. For a given gas, the breakdown voltage is a function only of the product of the pressure and gap length. The curve he found of voltage versus the pressure-gap length product is called Paschen's curve. (See Figure 2.) He found an equation that fit these curves, which is now called Paschen's law.

Figure 2. Paschen curves for varying pressures, courtesy Krishnavedala.

This has been mistaken to be a measure of resistance, which seems to become infinite at low pressures, but this is not correct. At higher pressures, the breakdown voltage increases steadily with pressure (off the right side of Figure 2), and so does the resistance. So there is a direct relationship between breakdown voltage and resistance in that range. If we erroneously take that as a hard and fast rule, and we observe the breakdown voltage shooting up at very low pressures, we conclude that the resistance must be increasing at very low pressures, asymptotically approaching infinite resistance at a pressure characteristic for that gas. But here we have to remember that Paschen was studying breakdown voltages, and made no mention of resistance. If we make direct measurements of the resistance, we find that it varies directly with the pressure, and continues straight down to nothing at no pressure, without the sudden deviation at the threshold discovered by Paschen. This can be confirmed by putting an ammeter into the circuit, and finding the resistance by the volts divided by the amps.

 

So why does the breakdown voltage shoot up at very low pressures, if the resistance is actually still decreasing?

 

The answer to that requires that we understand the nature of electric arcs. To get a spark, you need enough resistance to discourage an electric current. Then, ohmic heating from the current that is there (in glow mode) thins the gas, which increases the conductivity. This allows the passage of more current, meaning more ohmic heating, more thinning, less resistance, and thus more current. So it's a runaway breakdown of the capacitance of the gas. But what if there isn't enough resistance to prevent the flow of current in the first place, as is the case when the pressure is greatly reduced (or the gap is very small)? Then the current flows without having to break down the resistance. And the proof is on the ammeter.

 

For electrical engineers, the confusion is more deep-set. They think of electric currents as a domino effect in the electron cloud of a solid conductor. To estimate the current, you just find the electric potential (i.e., the volts), and divide that by the resistance typical for that particular conductor (i.e., the ohms). The resistance of a solid conductor can be predicted by the binding energy of the valence electrons. So copper, whose outer electrons are very weakly bound to the atoms, is an excellent conductor. Ask an EE about currents in gases or plasmas, and the response will be that there isn't a crystal lattice with an electron cloud, and therefore there won't be any current at all. Hence it really isn't that EEs actually think that free space is an insulator. It's that they just don't have a concept of a current flowing outside of a crystal lattice. If they absolutely have to deal with currents that are not totally solid-state (such as in vacuum tubes), the best they can do is start talking about the electrode's work function. What they don't realize is that if the properties of the electrode are the only things that affect the resistance in the vacuum tube, the vacuum itself simply doesn't have any resistance, and that's by definition. But for most EEs, currents stay in solid-state circuits, and any discharges that escape the confines of the wiring don't need theoretical explanations — they just necessitate replacement parts and/or a quick trip to the clinic for some burn ointments.

 

In plasma physics, this isn't good enough. Very real currents flow through gases & plasmas, and the resistance varies directly with the density. The drift speed of an electron through free space can be expressed in terms of the accelerating electric field, the electron mass, and the characteristic time between collisions.

 

Offsite Discussions

 

Comments:

 

My Problem with the Vacuum Conducting Electricity