© Lloyd

 

Testing a Mechanical Behavior of Light Reflection

 

http://www.worldnpa.org/site/abstract/?abstractid=7098&subpage=pdf

 

1. Introduction

 

We model photons and atoms as spherical rigid bodies and reproduce numerically the mechanical (Newtonian) interactions between them. Our goal is to analyze how the frequency of the photon varies depending on its interaction with the atoms. In our work, we compare numerical results against experimental results obtained in laboratory. To analyze the frequency variation of each photon, we assume the photon as being a spherical rigid body within nonuniform internal mass distribution, so that the photon describes a cycloid, as can be seen in Figure 1. Thus, once describing cycloids, our rigid body presents mass, amplitude, frequency and phase, as well as the DeBroglie (1924) wave and becomes a mechanical framework for our study case. To simulate this internal non-homogeneous mass distribution, we used a spherical rigid body within holes so that its centroid and its center of mass are not coincident. Thus, while the center of mass describes a straight line, the centroid describes a cycloid.

 

 

 

3. Modeling the collisions

 

To simplify our numerical model, we assume that the atom is stuck into a grid and do not move after the collision. This simplification avoids problems concerning vibration of the grid of atoms. Based on the estimates of photon mass of Rodriguez and Spavieri (2007); Williams et al. (1971); Chernikov et al. (1992); Davis and Nieto (1975); Franken and Ampulski (1971); Accetta et al. (1985); Crandall (1983); Lakes (1998); Fishbach et al. (1994); Schaefer (1999) and Luo et al. (2003), which estimates photon masses among 10-51kg and on the periodic table, which indicates the atomic mass of gold among 10-26kg, we assume that the mass of a photon is 1025 smaller than the mass of the atom, which means that any movement of atom is negligible when compared with the movement of the photon.

 

 

© Charles Chandler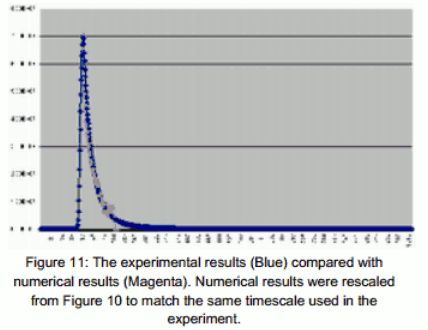

 

 

7. Conclusion

 

As can be seen in Figure 11, the time spent between the launch and the return of a spherical rigid body (assumed as representing a photon) presents a similar behavior as the quantum decay measured in the laboratory. We believe that light is ballistic and that its behavior of wave is caused by its non-homogeneous mass distribution, which generates cycloids and, consequently, a wave behavior. In order to test this model, we started to compare different behaviors of light. Recently (Sauerbronn et al., 2010), we tested this mechanical model of light against the single slit diffraction experiment and the numerical results were considered very similar to the experimental results. When testing this mechanical model of light to describe the behavior of colors (Sauerbronn et al., 2013) we found very interesting results. When testing this mechanical model of light against the behavior known as quantum decay, we found once again results that look similar to experimental results. Considering that we do not know the physical properties of a photon, we are trying different values for volume, geometry, mass etc intending to achieve one combination that fits perfectly all experimental results. That is the point where we are now. As a final remark, this work was inspired by the model of light of the atomist Lucretius (1992, 1995). Our contribution is in the proposal of a non-uniform distribution to the photon's internal mass and in the implementation of a numerical model to test this proposal against experimental results achieved by a experiment involving quantum decay.

 

8. Future Work

 

We believe that the photon is a drop. It requires heat to be produced, arises from a source and accelerates until reach its final speed. The photons have a melting point. The Planck's Law indicates the number of drops (on the vertical axis) and the kinetic energy levels of each drop (on the horizontal axis). As a future work, we intend to test these hypotheses. We also believe that nuclei of atoms are superconductors and that electrons are magnets. Instead of using orbitals, our chemical bonds are fully based on the Meissner effect where a network of magnets (electrons) connects the nuclei within a molecule. Each magnet (electron) connects two nuclei. As a second future work, we intend to test these hypotheses.