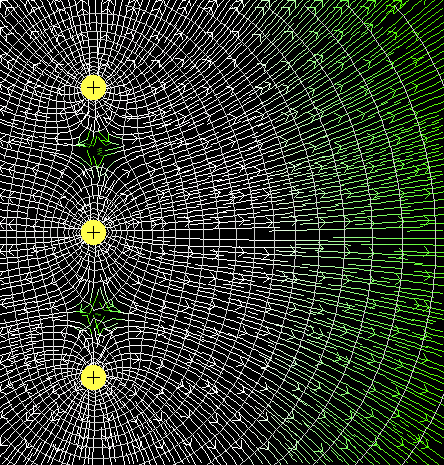
© Charles Chandler

 

But it was naïve of us (and Dalsgaard) to simply run out the ideal gas laws, assuming that pressure and temperature always define density. When dealing with extreme pressures, there is another factor that has to be taken into account: the Coulomb barrier. Compressing a gas (or plasma) is easy enough, until you get down to the density of a liquid, wherein all of the atoms have achieved a closest-packed arrangement. Further compression is much more difficult, as liquids are incompressible. This is because at the liquid density, the outer electron shells of neighboring atoms are in contact with each other. Further compression will cause the failure of those shells, expelling the electrons, and leaving the atoms ionized. Thereafter, electrostatic repulsion between the like-charged atoms pushes them apart. And since the electric force obeys the inverse square law, the repulsion increases exponentially with further compression. Hence we need to add the Coulomb force to the hydrostatic pressure before concluding that the model is in equilibrium.

 

We also need to add the electrostatic attraction between electrostatic layers. To understand why, let's do a thought experiment.

 

Consider that we have a box that measures 1 meter on all sides, filled with air. The air will be evenly dispersed within the box. Then we insert a divider into the box, to split the volume into two. The air is still evenly dispersed within each compartment. Suppose the divider is a perfect insulator, so no electric currents can flow through it, but it has a high permittivity, so electric fields can shine straight through it. We now take out our atomic tweezers, and one by one, we pick every electron out of the one side and put it into the other, and put every atom into the other compartment. Now we have one compartment with nothing but atomic nuclei on one side, and electrons on the other.

 

Now, with one compartment filled with nothing but positive ions, and the other with nothing but electrons, will the particles in each compartment be thoroughly dispersed due to electrostatic repulsion, or will they be concentrated in the center, as close as they can get to the divider, attracted to the opposite charge just on the other side?

 

The answer is both, but the latter is the more powerful force. The following images will help illustrate. First, we have three positive charges. Notice the collisions of lines of force between each ion. This is the source of the electrostatic repulsion between them.

 

 

 

Figure 1. Lines of force from three positive ions.

 

 

Now we add three complementary negative charges. Notice that most of the lines of force have been bent towards the opposite charges, and the field density between like charges is not as great. This means less electrostatic repulsion between the ions. And that means that they will be closer together. So it's not just that the ions will be attracted to the opposite charges, minus their repulsion from each other. There's less repulsion, due to the redirection of the lines of force. This allows the ions to get packed together more tightly. And the closer they get to the opposite charges, the electric force increases exponentially. So we will expect a major concentration of charges on either side of the divider, despite the repulsion of like charges within each compartment.

 

 

Figure 2. Lines of force with three positive and three negative charges.

 

 

Once the initial charge separation has been set up, we can then expect a third layer to form. The next image shows a solid conductor that has been added on the right side. Though the conductor would otherwise be neutral, it attracts the lines of force from the negative charges, and it becomes positively ionized, with an electric force pulling it toward the negative charges.

 

 

Figure 3. Solid conductor attracts lines of force.

 

 

So if the walls of our 1 meter box were conductors, and if they could move, they would get drawn inward, and it would no longer be 1 cubic meter of air — it would be a lot less, due to the electrostatic potential consolidating the matter. This is interesting because if the topic is the Sun, and if compressive ionization has set up charged double-layers, the compaction of the plasma will increase the density of the gravitational field. Furthermore, if gravity is the force responsible for the compressive ionization, and if such ionization makes the gravitational field more dense, then this constitutes a force feedback loop. The net result is that the plasma will be much more dense than the ideal gas laws would have predicted.