© Charles Chandler

 

The laws of hydrostatics tell us that the density, pressure, and temperature of gases (and plasmas) are all related, and that if we know 2 of them, we can calculate the third. So this is something that we can check.

 

We can also check that the pressure is realistic, given the force of gravity. For a discrete celestial object such as the Sun, density and pressure are not just related by temperature. The density of the matter generates the gravitational field that supplies the pressure necessary to compress the matter. So we can step through the following process:

1. Given the model densities of each parcel, calculate the force of gravity, from each parcel to each parcel, and add it all up to get the total gravity acting on that parcel. This is the parcel's weight.
2. A parcel's weight supplies the pressure that compresses the parcel below it. So normally, pressure is calculated from the known density & temperature, but here we can calculate the pressure just from the density, given the densities of all of the other parcels, and the force of gravity.
3. Knowing the calculated pressure, and the model temperature, we can recalculate the density. If the new density doesn't match the model density, the model is not correct.

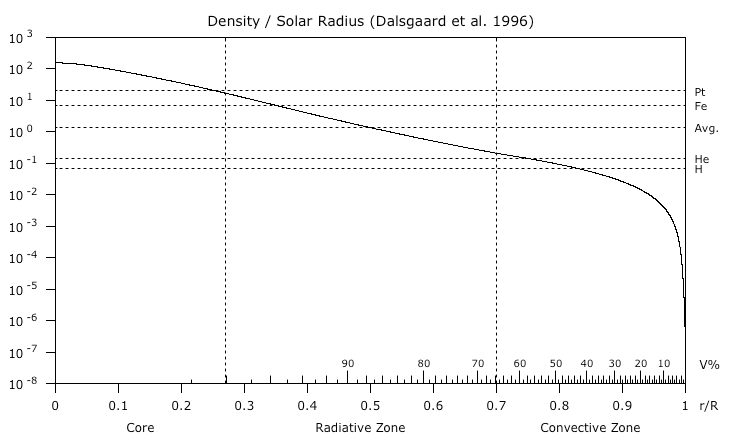
When all of this is done for the Dalsgaard model, asserting a 75/25 mix of hydrogen/helium, it all checks out. In other words, if those were the correct densities, pressures, and temperatures, gravity would put it all into hydrostatic equilibrium. (See Figure 1.)

 

 

Figure 1. Density per solar radius in the Dalsgaard model, based on the ideal gas laws, with gravity pulling in, and with heat from nuclear fusion in the core generating the hydrostatic pressure that pushes back out. The X axis shows the decimal of the solar radius starting from the center, and the percentage of the solar volume, starting from the surface. The Y axis shows g/cm³. The densities of liquid platinum, iron, helium, and hydrogen are shown for reference. The average density of the Sun is 10^0.15 = 1.408 g/cm³ = 1408 kg/m³.

 

 

But it doesn't produce any internal helioseismic boundaries, nor a distinct limb, much less the granular dynamics on the limb.