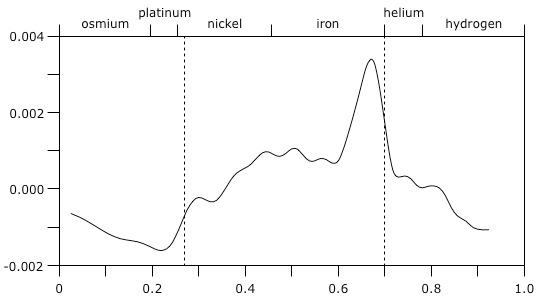
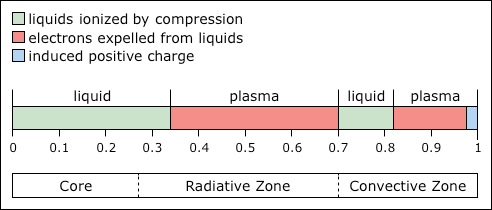
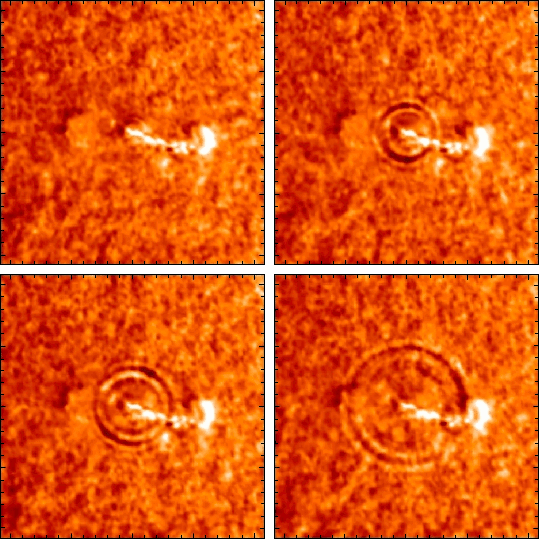
© Charles Chandler

 

There is one other type of data that can be used to refine this analysis. There are slight anomalies in the transmission speeds of sound waves through the Sun, as shown in Figure 1.

 

 

Figure 1. Anomalies in the transmission speeds of p-waves per solar radius, courtesy Stanford University.

 

 

It's possible that these are evidence of differences in density and charge.

 

 

Figure 2. Physical states and layers of charge in the Sun, due to EDP and induction.

 

 

Starting from the top and descending into the Sun, we see a distinct increase in transmission speed at .85 R_⊙. This corresponds with the liquid hydrogen line, where the waves travel faster in the liquid. Then we see a very sharp spike at .65 R_⊙, which is the top of the iron layer. This should be in the plasma state, but it should be hot, high-pressure plasma, due to arcs across the charge separation at .7 R_⊙.

 

The largest dip, just inside the core, could be simply the result of the increase in density. The bottom of the nickel layer, and everything below it, is ionized liquid, so the transmission speeds should be more or less the same, but increases in mass will slow down the waves.

 

Figure 3. Seismic shadows due to differences in density.

Note also that the "model" for transmission speeds had to be developed heuristically, as observations do not obey standard fluid dynamic principles. The depth of the boundaries can be computed based on refraction shadows created by density changes in the Sun, the way it normally would. (See Figure 3.) So this is fairly reliable. But the expectations for the speed of sound rely on many factors to which we have no direct access, such as the elementary composition, temperature, and degree of ionization.

 

As an indication of how influential ionization can be, we can observe the behavior of s-waves propagating through the photosphere, as in Figure 4. The scientists who studied this event made an interesting observation.

Unlike water ripples that travel outward at a constant velocity, the solar waves accelerated from an initial speed of 10 km/s to a maximum of 100 km/s before disappearing.

So the waves started at a supersonic speed, and then accelerated by another order of magnitude? That breaks two laws of hydrodynamics. (A third is broken if we expect s-waves to occur in plasma that the standard model claims is as thin as the best laboratory vacuum on Earth.^1:73) This can only mean that the surface has a net charge, where the motion of one particle begins to accelerate the next particle even before they collide, by electrostatic repulsion, thus enabling the propagation of waves faster than the speed of sound. (This is also one of the indicators that the net charge in the photosphere is positive. If those were negative ions, and if a pressure wave was initiated, an ion moving closer to another ion and experiencing a repulsive force would simply lose the electron, with little effect on the momentum of the nuclei involved in the collision. In other words, in highly conductive plasma, electrons can move from atom to atom quite freely if there is any voltage at all, and similarly, the atoms can move for their own reasons, leaving the electrons behind if the voltages prefer it that way. But in a positive ion, the inertial and electric forces stem from the same entity, and cannot be disassociated in the same way. So a supersonic, accelerating pressure wave is proof of a positive charge.)

 

 

Figure 4. Waves propagating after a solar flare, 1996-07-09. The images show an area 200 Mm across.

© 1998 SOHO

 

 

This explains why all of the transmission speeds are far greater than what is predicted by standard fluid dynamics.